ВЫБОР РАЦИОНАЛЬНОЙ СХЕМЫ ПРОДОЛЬНОЙ ПОДАЧИ ПРИ CBN-ШЛИФОВАНИИ ПЛОСКИХ ДЕТАЛЕЙ ИЗ СТАЛИ 08Х15Н5Д2Т

 

SELECT OF ACHIEVEMENT WAYS OF A LINE FEED BY THE CBN-GRINDING OF FLAT PARTS FROM THE STEEL OF 08Cr15Ni5Cu2Ti

 

Солер Я.И., Стрелков А.Б, Митюхляева О.С., Ширяев П.Б.

(НИ ИрГТУ, г. Иркутск, РФ)

Soler Ya.I., Strelkov A.B., Mityukhlyaeva O.S., Shiryaev P.B.

(National Research Irkutsk State Technical University, Irkutsk)

 

С использованием параметрических и непараметрических методов статистики исследовано влияние способа задания продольной подачи на параметры микро- и макрогеометрии при CBN- шлифовании плоских деталей из стали 08Х15Н5Д2Т.

The effect of achievement ways of a line feed was researched using the parametric and nonpararametric statistics on the surface micro- and macrogeometrics by griding CBN wheel.

Ключевые слова: шероховатость, шлифование нитридборовым кругом, продольная подача, статистика

Key words: roughness, CBN grinding, line feed, statistics.

 

На данный момент в нормативных документах отсутствуют рекомендации по выбору схемы задания продольной подачи. На практике возможно использование двух схем плоского шлифования периферией круга для рабочего хода при поперечной подаче на двойной ход: попутное и встречное (терминология заимствована из фрезерования цилиндрической фрезой) без учёта роли обратного выхаживающего прохода. Об эффективности использования той или иной схемы до сих пор не существует единого мнения. Так, в [1] установлено, что пиковая температура выше при попутной схеме обработки, но растёт она медленнее, чем при встречном, а возникающие при этом усилия на 80 % выше. Влияние схем резания на качество шлифованной поверхности деталей, по нашим данным, до сих пор ни кем не исследовано.

Опыты вели при следующих неизменных условиях: плоскошлифовальный станок модели 3Г71М; круги из кубического нитрида бора 1А1 200×20×76×5 CBN 30 160/125 СТ1 К27 100 (производитель – ОАО «НПК «Абразивы и Шлифование», г. Санкт-Петербург); технологические параметры- скорость круга v_к=28 м/с, продольная подача s_пр=6 м/мин, глубина резания t=0,005 мм, операционный припуск z=0,1 мм; СОЖ-5%-ная эмульсия Аквол -6 (ТУ 0258-024-00148843-98), подаваемая поливом на деталь в количестве 7-10 л/мин. Шлифование вели по торцу заготовки из коррозионно-стойкой стали 08Х15Н5Д2Т (ВНС-2) (,  ) с размерами D×L=30×40 мм и повторением наблюдений n=30. Варианты реализации продольной подачи (): 1– встречное; 2– попутное. Состояние микрорельефа деталей оценивали параметрами: R_a, R_z, R_max и ,  (ГОСТ 25142-82) в двух взаимно ортогональных плоскостях с использованием измерительной системы на базе профилографа-профилометра «Абрис ПМ-7». Макрогеометрию плоской поверхности оценивали параметрами (ГОСТ 24642-81) EFE и TFE с помощью микрокатора 2-ИПМ (ТУ 2-234-229- 89) с ценой деления 1 мкм [2].

Обработка результатов исследования проведена с помощью программы Statistika 6.1.478 по методике [3], которая схематично представлена на рисунке 1, в предположении того, что выходные параметры процесса следует рассматривать случайными величинами (СВ) [4]. Выходные параметры процесса с учётом условий шлифования представим в виде последовательностей

,,                                                                                (1)

которые позволяют отыскать следующие характеристики в эмпирических распределениях: меры положения (опытные средние  и медианы ); меры рассеяния (стандарты отклонений  или их дисперсии , размахи , интерквартильные широты - ; меры формы этих распределений, например симметричное и асимметричное.

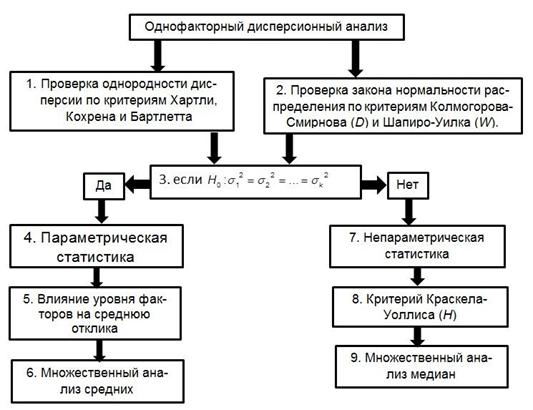
Рисунок 1- Алгоритм поиска наиболее вероятных значений случайных величин

 

Классический дисперсионный анализ (ДА) основан на предположении, что наблюдаемые СВ имеют гауссово распределение с одинаковыми дисперсиями (этапы 1-2 на рисунке 1) [5]. Однако изучаемые наблюдения далеко не всегда подчиняются закону нормального распределения. В такой ситуации правомерно возникают вопросы: насколько корректным оказывается применение классического аппарата ДА «на чужом поле» [6]. В таком случае теоретическая статистика рекомендует воспользоваться непараметрическими методами которые не накладывают ограничений на СВ (меньшая чувствительность к «шумам»), обладают меньшей чувствительностью к грубым ошибкам, попавшим по той или иной причине в случайную выборку.

Для оценки стабильности процесса шлифования использовано соотношение:

k_SD=(SD_баз)/(SD_i)                                                    (2)

где SD_баз и SD_i - соответственно выборочные стандарты отклонений базового и сравниваемого вариантов (оценки ).

Так, при k_SD<1 в (2) имеем стабильность базовой схемы обработки выше, чем при иных условиях шлифования.

При проверке на гомогенность распределений по критериям Хартли, Кохрена и Бартлетта установлено, что условие 3 (рисунок 1) не выполняется лишь для параметров  и . Проверка закона нормального распределения по критерию Шапиро-Уилка, как наиболее строгому по сравнению с критерием Колмогорова-Смирнова, выявила нарушение нуль-гипотезы о нормальном распределении СВ для всех исследуемых параметров. Для гистограмм наблюдений (1) для параметров шероховатости R_a1i (рисунок 2) имеем надёжности выполнения нуль-гипотезы: α₁=0,002, α₂=0,06 при допустимом нижнем пределе 0,5 [7]. Это определило целесообразность использования непараметрических методов статистики. Результаты интерпретации (1) на базе параметрических статистик приведены для оценки их состоятельности на «чужом поле» [6].

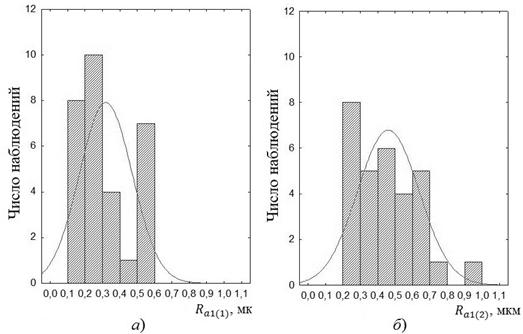
Рисунок 2 - Гистограммы наблюдений (1) для параметра ,  с наложением кривых нормального распределения: а – s_пр встречное; б – s_пр попутное

 

В таблице и на рисунке 3 приведены результаты сводного внутригруппового параметрического анализа для параметра R_a1i, . Установлено, что встречное шлифование позволяет снизить шероховатость поверхности по мерам положения средних для параметра R_a1 в 1,4 раза. Однако в связи с нарушением 2 (рисунок 1) предпочтение следует отдать результатам непараметрического анализа, по результатам которого снижение шероховатости по мерам положения медиан предсказано в 1,7 раза. В категориальных величинах (КВ) размах колебаний при встречном и попутном шлифовании составил 7 единиц размерного ряда, хотя абсолютные значения границ размаха наблюдений (1) при попутном шлифовании соответствуют большим величинам. По (2) первый вариант задания s_пр подтвердил изложенные выше результаты: i=1 - k_SD=1; i=2 - k_SD=0,85. Эти результаты хорошо согласуются с доверительными интервалами при надёжности оценок на 5%-ом уровне значимости: две КВ при i=1; 3 КВ при i=2. Аналогичные результаты отмечены для остальных высотных неровностей в обоих направлениях.

 

Таблица 1 - Сводный внутригрупповой дисперсионный анализ для параметра R_a1i

 

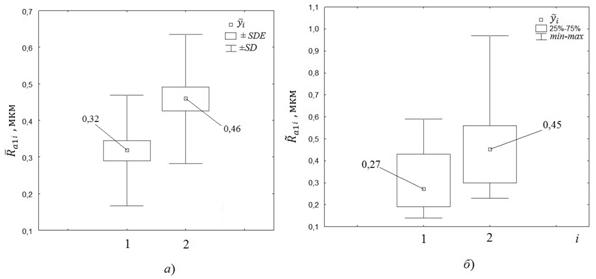
Рисунок 3 - Описательные параметрические (а) и непараметрические (б) статистики для параметров R_a1i

 

Выявлено значимое влияние схемы врезания на параметр t_p который по ISO 13565 [8] влияет на различные эксплуатационные свойства деталей: p≤20% - на интенсивность приработке трущихся поверхностей соединений,  - на их несущую способность. В частности, величина поперечного параметра  оценивается величинами: 37,5 % при попутном шлифовании (i=2); 43,3 % для альтернативной схемы (i=1). При этом в ряде сечений t_p,  отмечено снижение значений опорных длин от 33 % (i=2) до 12 % (i=1), что предсказывает увеличение интенсивности износа поверхности в начальный период приработки при работе по встречной схеме.

По результатам непараметрических оценок было установлено, что схема врезания значимо влияет на отклонение от плоскостности EFE: прогнозируемое значение  при попутной схеме (i=2) составило 7 мкм (TFE6), а при встречной 1 - 6 мкм (TFE5). Так же при встречной схеме достигается большая стабильность отклонений от плоскостности для операционной партии по (2): при i=1 - k_SD=1; при i=2 - k_SD=0,51. Полученные результаты по k_SD совпадают с стабильностью параметров шероховатости поверхности деталей. Это позволяет при шлифовании коррозионностойких сталей мартенситного класса для снижения параметров микро- и макрогеометрии рекомендовать встречную схему врезания круга в деталь (i=1).

 

Список использованных источников

1.  Badger J. Deciding whether up or down grinding is right for an application // Cutting Tool Engineering, Vol. 56, N8 2004, pp. 68-70.

2.  Солер, Я.И. Прогнозирование макрогеометрии деталей из стали 13Х15Н4АМ3 при плоском шлифовании кругами из кубического нитрида бора / Я.И. Солер, А.Б. Стрелков, Д.Ю. Казимиров // Справочник. Инженерный журнал. – 2009. – №11. – С.26-37.

3.  Солер, Я.И. Выбор абразивных кругов при плоском шлифовании деталей силового набора летательных аппаратов по критерию шероховатости поверхности / Я.И Солер, Д.Ю. Казимиров // Вестник машиностроения. – 2010. - №3 - С.55-64.

4.  Солер, Я.И. Исследование влияния выхаживания на микрорельеф пластин Р9М4К8 при шлифовании кругами из кубического нитрида бора / Я.И. Солер, А.В. Прокопьева. Обработка металлов. - 2009. - №1- (42).- С. 24-27.

5.  Шеффе, Г. Дисперсионный анализ / Г. Шеффе: пер. с англ. - М.: Физматтиз, 1980. - 628 с.

6.  Холлендер, М. Непараметрические методы статистики / М. Холлендер, Д. Вулф. Пер. с англ. - М.: Наука, 1983. - 518 с.

7.  Поллард, Дж. Справочник по вычислительным методам статистики / Дж. Поллард. Пер. с англ.  М.: Финансы и статистика, 1982. - 344 с.

8.  Кремень, З.И. Технология шлифования в машиностроении / З.И. Кремень, В.Г. Юрьев, А.Ф. Бабошкин; под ред. З.И. Кремня. -СПб: Политехника,  2007.- 424 с.