Разработка адаптивного вибрационного привода

РАЗРАБОТКА АДАПТИВНОГО ВИБРАЦИОННОГО ПРИВОДА

DEVELOPMENT OF AN ADAPTIVE VIBRATION DRIVE

Шугаев Г.А. (Восточно-Казахстанский государственный университет им. Сарсена Аманжолова г.Усть-Каменогорск, Казахстан)

Shugayev G.A. (East-Kazakhstan State University named after S. Amanzholov, Ust-Кamenogorsk, Kazakhstan)

Рассмотрены вопросы по применению адаптивных вибрационных приводов в промышленности.

Issues of adaptive vibration drive application in industry have been considered

Ключевые слова: адаптация, машиностроение, привод

Keywords: adaptation, machine-building, drive

Разработка адаптивного вибрационного привода, обеспечивающего при постоянной входной мощности переменную скорость движения выходного рабочего органа, в зависимости от нагрузки на нем, и создание вибрационного воздействия на рабочий орган, является актуальным решением в преодолении стартового сопротивления в начале движения и перегрузок в эксплуатационном режиме движения машины[1,2,3].

Адаптивный вибрационный привод способен обеспечить уменьшение мощности, габаритов и веса, а также плавность работы машинного агрегата[4,5].

Особенно важно использовать адаптивные приводы в тех механизмах, где отказ исполнительного механизма при движении может привести к аварии.

Настоящая работа посвящена разработке адаптивного привода и исследования выполняются на основе законов механики.

Движение материальной точки при наличии упругой связи

Система с упругим контуром будет иметь такой характер движения, который ранее не рассматривался. Поэтому сначала рассмотрим простейший случай движения подпружиненной материальной точки.

Рассмотрим движение материальной точки при наличии упругой связи

Предлагается изменить классическую постановку задачи анализа колебательного движения материальной точки под действием сил для поиска возможных новых механических эффектов.

Постановка задачи.

Рассмотрим движение материальной точки с массой под действием движущей силы , передаваемой через пружину сжатия с жесткостью и силы сопротивления (рисунок 1). Точка приложения силы перемещается равномерно. Определим закон движения точки .

Предположим, что движущая сила постоянна по величине и равна силе сопротивления. В этом случае движущая сила и сила сопротивления вызывают статическое укорочение пружины Следовательно .

Если сила сопротивления больше движущей силы на величину , то движение точки относительно точки (перемещение ) будет происходить под действием силы и восстанавливающей силы . Здесь - абсолютные перемещения точек и .

При этом следует иметь в виду, что постоянная сила не изменяет характера колебаний, совершаемых точкой под действием восстанавливающей силы , а только смещает центр этих колебаний в сторону действия силы на величину соответствующего статического отклонения . В этом случае восстанавливающая сила и .

Рассмотрим общий случай движения системы.

Перемещение точек системы можно рассматривать в виде двух последовательных фаз. Фаза 1 – движение точки при неподвижной точке , приводящее к сжатию пружины или к ее зарядке.

Фаза 2 - движение точки при неподвижной точке , происходящее вследствие разрядки пружины. Чередование фаз зарядки и разрядки пружины приводит к непрерывному движению системы при сохранении упругого взаимодействия сил вне зависимости от времени.

Движущая сила постоянна по величине и не равна силе сопротивления. Движущая сила и сила сопротивления вызывают статическое укорочение пружины

Следовательно .

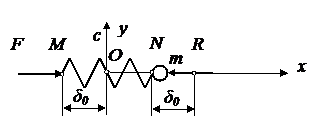
Рисунок 1 - Движение подпружиненной материальной точки под действием сил

Разместим точку начала координат в положении статического равновесия на расстоянии от точки . После перемещения точки приложения силы в точку восстанавливающая сила начнет перемещать точку вправо в новое положение равновесия на расстоянии от точки.

Восстанавливающая сила равна силе упругости пружины

. (1)

Точка перемещается из исходного положения равномерно.

Уравнение движения точки имеет вид:

, (2)

где – время, - скорость точки , – время цикла.

Дифференциальное уравнение движения точки, которую перемещает восстанавливающая сила, имеет вид:

. (3)

Подставив в уравнение (3) значения сил, получим: .

Обозначим (–частота колебаний). Тогда получим дифференциальное уравнение гармонических колебаний точки

. (4)

Период колебаний точки

. (5)

Решение дифференциального уравнения (4) имеет вид:

. (6)

Для точки по начальным условиям при .

Здесь – скорость точки .

(7)

Подставляя в формулы (6) и (7) начальные данные, получим:

Следовательно, согласно уравнению (6) для точки колебания происходят с амплитудой по закону:

. (8)

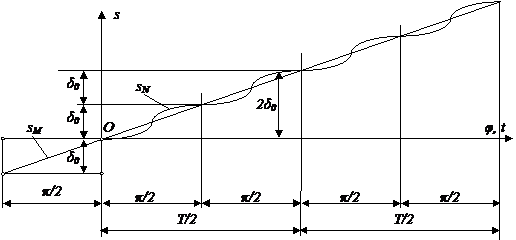
Рисунок 2 - Графики перемещения точек системы

В рассматриваемом случае в отличие от обычных колебаний по истечении половины цикла движение точки продолжается в первоначальном направлении, то есть происходит повторение движения первой половины цикла. Это означает, что угол имеет одинаковые пределы изменения в первой и во второй половине цикла: , начало отсчета перемещений второй половины цикла соответствует концу первой половины цикла. Следовательно, для второй половины цикла формула (8) примет вид

. (9)

Здесь – перемещение точки за период времени.

Графики перемещений точек представлены на рис. 2.

Следует отметить, что уравнение движения материальной точки можно получить, рассматривая обычную модель колебательного движения этой точки при неподвижной точке (рисунок 1) в инерциальной системе отсчета, движущейся с постоянной скоростью .

Выполненные исследования позволяют сделать вывод о возможности передачи непрерывного однонаправленного движения с помощью упругой связи. Передача движения происходит путем создания периодических импульсов.

Динамика рычажного механизма с замкнутым упругим контуром

Постановка задачи исследования рычажного механизма с замкнутым упругим контуром: на основе найденных закономерностей колебательного движения материальной точки разработать условия обеспечения передачи движения на выходной рабочий орган упругими импульсами.

Следует отметить, что передача движения с использованием гармонических колебаний должна использовать вынуждающие силы для поддержания постоянного характера колебаний. Создание переменной по величине вынуждающей силы может быть выполнено с помощью внешнего механизма, обеспечивающего неравномерное движение выходного звена, приводящего входное звено адаптивного механизма. Однако замкнутый контур адаптивного механизма способен самостоятельно создавать переменные вынуждающие силы, что приводит к появлению автоколебаний. Согласно теореме о механической адаптации на промежуточных звеньях замкнутого контура действуют неравные по величине силы, которые вызывают соответствующие ускорения и силы инерции. При этом имеет место связь между силами инерции по принципу возможных перемещений. Наличие указанной связи приводит к появлению переменной вынуждающей силы.

В настоящей работе рассмотрены в качестве начального исследования закономерности движения материальной точки без использования вынуждающей силы.

Для каждого упругого звена в контуре можно использовать найденные закономерности движения материальной точки, заменив соответствующие параметры, используемые в динамике точки на параметры звена. Для обеспечения координации движений звеньев необходимо ввести дополнительное условие равенства их частот колебаний. При этом движение каждого звена будет иметь колебательный характер, а связь между перемещениями точек звеньев в любой момент времени будет соответствовать картине перемещений точек (рисунок 3).

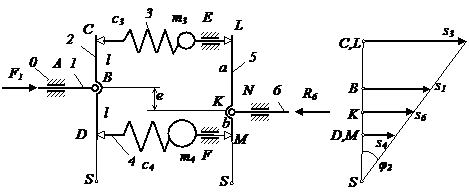
Рисунок 3 - Рычажный механизм с упругими звеньями и картина его перемещений

Для звеньев 3 и 4 в формулах: 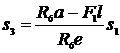(10)

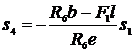(11)

определяющих перемещения точек звеньев, следует принять при за период времени.

Движение точек звеньев 3, 4 происходит в соответствии с уравнением (2):

, (12)

. (13)

Движение точек звеньев 3, 4 происходит в соответствии с формулой (3):

, (14)

. (15)

Эти уравнения в соответствии с формулой (4) приводятся к виду:

. (16)

. (17)

Решения дифференциальных уравнений движения (16), (17) в соответствии с формулой (8) приводятся к виду:

, (18)

, (19)

где – статические укорочения пружин звеньев 3, 4,

– частоты колебаний пружин

. (20)

Полное перемещение в одном направлении в течение половины цикла .

Точки упругих звеньев 3, 4 под действием сил совершают гармонические колебания. Для согласованной работы пружин необходимо выполнение условия . Отсюда следует условие подбора масс:

. (21)

Время одного цикла, включающего зарядку и разрядку пружин, равно:

. (22)

Скорости звеньев с учетом совершения каждой фазы (зарядки и разрядки) за цикл:

, , . (23)

Колебательный характер движения точек звеньев 3, 4 обеспечивает характер движения звеньев механизма внутри контура. Это движение не зависит от длин пружин, то есть не зависит от продолжительности работы. При этом для механизма в целом сохраняются связи по формулам: (24), (10), (11).

Найденные выражения позволяют определить движение всех точек, параметры этого движения и характеризуют определимость движения механизма с двумя степенями свободы при наличии только одного входного звена и при отсутствии потерь энергии на трение (за исключением потерь в пружинах на внутреннее трение).

Частота колебаний в упругом контуре высока и имеет вибрационный характер, что в сочетании с эффектом силовой адаптации предопределяет высокую надежность трогания с места за счет вибрационного воздействия на выходной рабочий орган. В эксплуатационном режиме вибрационное воздействие сглаживается наличием необходимой массы выходного звена.

Выводы:

Выполненные научные исследования позволяют создать простой и надежный адаптивный вибрационный привод сервисного механизма.

Выполненные научные исследования позволяют создать простой и надежный адаптивный привод для различных отраслей промышленности.

Заключение. Силовая адаптация приводит, во-первых, к обеспечению плавности движения, и, во-вторых,- к существенному уменьшению ускорений и связанных с ними инерционных нагрузок.

Мощность адаптивного привода при постоянной (неизменной) входной скорости меньше мощности обычного привода в несколько раз. Соответственно имеют место соотношения между габаритами и весом адаптивного и обычного приводов.

Адаптивный привод использует свойства механизма с двумя степенями свободы и не требует применения управляющих устройств для изменения передаточного отношения.

Адаптивные приводы технологических машин с переменным сопротивлением движению обладают несомненными преимуществами по сравнению с обычными.

Рисунок 4 - Устройство для нагрева семян подсолнечника

Устройство для нагрева семян подсолнечника с непрерывным циклом производства (рисунок 4). Использование адаптивного вибрационного привода качественно обеспечило стабилизацию технологического процесса, увеличило выход годного продукта, повысило надёжность всего устройства. Данная установка внедряется на одном из частных маслозаводов Восточно-Казахстанской области. Автор и разработчик проекта Шугаев Г.А.

Литература

1. K.S.Ivanov. Discovery of the Force Adaptation Effect. // Proceedings of the 11th World Congress in Mechanism and Machine Science. V. 2. April 1 - 4, 2004, Tianjin, China, p. 581 - 585.

2. Шугаев Г.А. Разработка адаптивного вибрационного привода.//

«Поиск». Научное приложение международного журнала «Высшая школа». - Алматы, 2009,- №4.- C. 292 - 299.

3. Shugayev G.A. Development of a gear stepless box with a clutch of ganging.// Proceedings of the 3rd International conference “Power transmissions 2009”. - Kallithea, Greece, - 2009. - С. 579 – 584.

4. Шугаев Г.А. Материалы Международного молодежного форума «Постиндустриальный мир: Наука в диалоге Востока и Запада», Усть-Каменогорск, Республика Казахстан,- 2011.-С.120-126.

5. Иванов К.С., Ярославцева Е.К., Шугаев Г.А. Устройство передачи энергии с непрерывно переменным передаточным отношением. Патент РК № 24625.