КИНЕМАТИКА ЭВОЛЬВЕНТНОЙ ЗУБЧАТОЙ ПЕРЕДАЧИ ПРИ НАЛИЧИИ ЭКСЦЕНТРИСИТЕТА КОЛЕС

 

Рудницкий В.Н. (БГИТА, г.Брянск, РФ)

 

We consider a gear with involute tooth profile, wheels which have the same geometric eccentricity. The presence of eccentricity leads to fluctuations in the transmission ratio.

 

В практике встречаются механизмы для передачи вращательного движения с переменным отношением угловых скоростей, состоящие из обычных колес 1 и 2 с эвольвентным профилем зуба, оси вращения А и В которых смещены на одинаковые расстояния е по отношению к геометрическим центрам О₁ и О₂, (см. рис. 1).

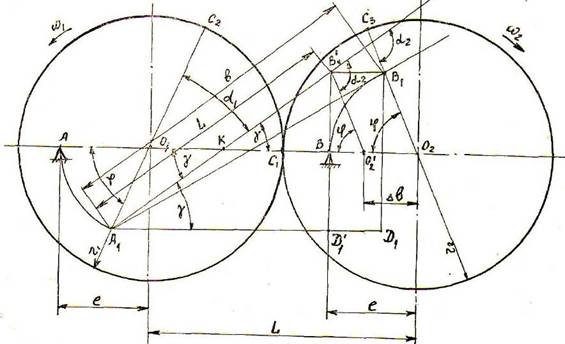
Рисунок 1 - Зацепление зубчатых колес, имеющих одинаковый эксцентриситет

 

Для определения характера изменения угловой скорости w₂ колеса 2 при условии, что скорость колеса 1 w₁=const, придадим вращение колесам 1 и 2 вокруг геометрических центров О₁ и О₂. Тогда, исходя из условия правильного зацепления, при повороте колеса 1 на угол φ колесо 2 повернется тоже на угол φ (︶C1С2 =︶C1С3).

Новым положе­ниям А и В будут соответствовать точки А1 и В1. Расстояние между точками А1 и В1 не равно расстоянию между точками А и В, что проти­воречит одному из условий, поставленных вначале. Проведем дополнительные построения, основываясь на поставленных ранее условиях. Для этого из точки В₁ проведем прямую, параллельную АВ, а из точки А₁ радиусом, равным АВ, делаем засечку на проведенной прямой. Полу­чим точку В₁'. Иначе, переносим колесо 2 по линии геометрических центров О₁О₂ на величину В₁В₁'  так, что величина А₁В₁' становится равной АВ.

Смещение геометрического центра колес в ту или иную сторону по линии центров О₁ О₂ нарушает контакт зубьев колес. Для возобнов­ления контакта требуется повернуть одно из колес на угол, равный Δφ. Угол Δφ есть величина переменная, как по абсолютной величине, так и по знаку. Отсюда можно судить о том, что:

                                            .                                          (1)

Зависимостью (1) в первом приближении можно пренебречь.

Из рис. 1 видно, что колесо 1 относительно прямой А₁В₁ поверну­лось на угол α₁, а колесо 2 на угол α₂. Из треугольников А₁О₁К  и  KB₁'0₂' следует, что

                                 , .                               (2)

Для Δ A₁В₁'D₁' справедливо равенство

                                        ,                                      (3)

где ;  значение  будет равно

                                         .                                               (4)

Основываясь на построениях рис. 1, получим                       

                                                                                     (5)

или с учетом   из (4)

                                     .                             (6)

Зацепление двух круглых колес с эксцентриситетом будет непре­рывным лишь в том случае, если выполняется неравенство

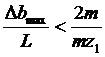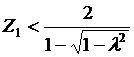                            или ,                           (7)

где т — модуль зубчатого колеса.

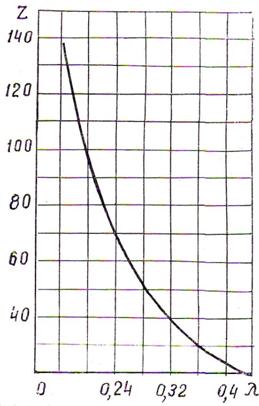
На рис. 2 показаны области использования рассматриваемой пе­редачи. Нижний предел z₁ = 17 может быть расширен при использо­вании колес с корригированными зубьями.

Продифференцируем (3) и подставим значение

                                  .                               (8)

После преобразования получим

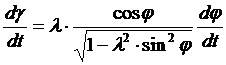                             .                                    (9)

Подставив (5) в уравнения (2) (предварительно продифференци­ровав их), получим значения угловых скоростей колес

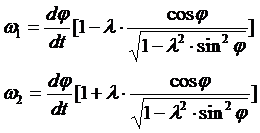                         .                       (10)

Отсюда передаточное отношение

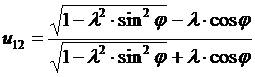                             .                     (11)

Рисунок 2 - Область использования рассматриваемой передачи

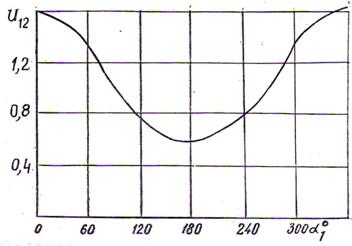
Рисунок 3- Графики зависимости передаточного числа и12 от угла α1

 

На рис. 3 показано, как изменяется передаточное отношение в за­висимости от угла α₁ при λ = 0,235. Из графика видно, что применение эвольвентных зубчатых колес с соответствующим геометрическим экс­центриситетом позволяет получить необходимый интервал изменения передаточного числа.

Полученные уравнения позволяют определить  передаточное отношение зубчатой передачи в зависимости от величины эксцентриситета эвольвентных зубчатых колес. Из приведенных графиков видно, что применение колес с эксцентриситетом позволяет получить передачи с меняющимся передаточным отношением в пределах, зависящим от величины эксцентриситета.