ОСТАТОЧНЫЕ НАПРЯЖЕНИЯ В ФЕРМЕННЫХ КОНСТРУКЦИЯХ ПОСЛЕ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ

 

RESIDUAL STRESSES DUE TO PLASTIC DEFORMATION IN TRUSS STRUCTURES

 

Круль Р. (Радомский Политехнический Университет им. Казимежа Пулаского, г. Радом, Польша)

 

В статье рассмотрен пример ферменной конструкции, в которой происходит пластическая деформация. После нагружения до предела текучести и разгрузки в стержнях вычислены остаточные напряжения.

 

This article presents the example of the truss structure under elasto-plastic deformation. The main aim in this article is computation of residual stresses after loading to the yield stress and unloading.

 

Ключевые слова: остаточные напряжения, ферменные конструкции

Keywords: residual stresses, truss structures

 

Остаточные напряжения возникают в процессе обработки деталей поддающихся воздействию резких температурных изменений, пластической деформации или после металлургических процессов. После таких видов обработки как ковка, штамповка, пайка или обдувка дробью в материале возникает пластическая деформация, вследствие которой изменяется объем материала и, после снятия внешних нагрузок, остаются остаточные напряжения. В некоторых источниках [1, 2] классификацию этих напряжений разделяют на три группы. Две из них относятся к микронапряжениям, которые изменяются в пределах размеров зерна или связанны с напряжениями в кристаллической решетке. В статье рассматриваются только макронапряжения, которые по сравнению с остальными группами классификации, изменяются незначительно в пределах размера зерна металла.

Важным свойством остаточных напряжений является их самоуравновешенность. В эпюрах, представляющих эти напряжения, равнодействующие усилия и моменты равны нулю [1].

В практике остаточные напряжения имеют положительные и отрицательные свойства. Наличие этих напряжений в поверхностных слоях некоторых хрупких материалов (например, стекло) может предотвращать их разрушение в случае поверхностного дефекта. С другой стороны нужно взять в учет что причиной разрушения некоторых деталей может быть суммарный эффект от внешних нагрузок и внутренних остаточных напряжений.

В некоторых случаях монтажные напряжения тоже можно считать остаточными. Если рассматривать соединенные детали по отдельности, то нужно считать что напряжения появились по причине внешних нагрузок и их нельзя считать остаточными. Если рассматривать соединенные части как одну целую, то возникшие монтажные напряжения можно считать остаточными напряжениями и нужно их взять в учет при анализе прочности конструкции прибавляя к напряжениям от внешних нагрузок [2]. На рис. 1. представлена схема образования остаточных напряжений после пластической деформации.

 

Рисунок 1- Схема образования остаточных напряжений σ_R после пластической деформации, σ – напряжения, ε – деформация, σ_T – предел текучести материала, tg(α) – модуль упругости, tg(β) – модуль упрочнения

 

После нагружения детали до предела текучести материала (отрезок AB), происходит пластическая деформация (BC). Разгрузка происходит по прямой CD и в случае, если во время этой разгрузки не произойдут другие пластические деформации, то остаточные напряжения будут равны σ_R. В примере, представленном на рис. 2 разгрузка происходит в пределах упругих деформаций и это дает возможность воспользоваться теоремой о разгрузке. Согласно этой теореме остаточные напряжения равны разности между напряжениями, возникшими в упруго-пластическом теле и теми, которые возникли бы в идеально упругом материале.

Рассчитываемая ферменная конструкция представлена на рис. 2. Параметры составных стержней конструкции находятся в таб. 1.

 

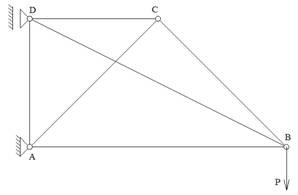
Рисунок 2- Статически неопределимая ферменная конструкция, для которой рассчитаны остаточные напряжения. Действующая в узле B сила P=22522N вызывает пластическую деформацию в стержне DC

 

Таблица 1- Параметры стержней ферменной конструкции представленной на рис. 2

Обозначение стержня	Длина [мм]	Модуль упругости [МПа]	Поперечное сечение [мм2]	Предел текучести [МПа]
AB	2000	200000	100	300
BC	1414
CD	1000	Модуль упрочнения [МПа]
DA	1000
DB	2236	2000
AC	1414

 

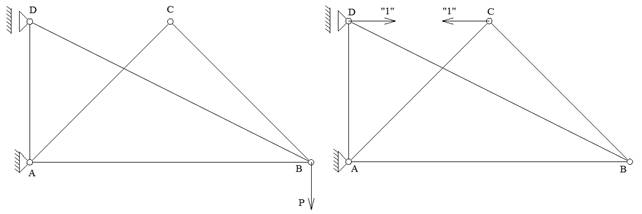
Рисунок 3- Статически неопределимая ферменная конструкция из рис. 2 в нулевом (слева) и единичном (справа) состояниях

 

Таблица 2- Силы в стержнях ферменной конструкции (рис. 2), L=1000 мм, P – сила в узле B

Обозн. стержня	Состояние „0”	Состояние „1”	длина	Сост. „0” умножен-ное на сост. „1”	Сост.”1” умножен- ное  на сост. „1”	Силы в действите-льном состоянии рис. 2
AB	-2P	0.5	2L	-2PL	0.5L	-1.32P
BC	0	0.707	L√2	0	0.707L	0.961P
CD	0	1	L	0	L	1.36P
DA	-P	0.5	L	-0.5PL	0.25L	-0.32P
DB	2.236P	-1.118	L√5	-5.59PL	2.795L	0.718P
AC	0	-0.707	L√2	0	0.707L	-0.961P

 

Из таб. 2 видно, что самая большая сила после нагружения возникнет в стержне CD (1.36P). Пластическая деформация появится в первую очередь в этом элементе. Сила P_T,CD, при которой возникнет пластическая деформация, вычислена в формуле (1).

                                   (1)

где σ_T – предел текучести материала, F – поперечное сечение стержней.

В таб. 3 даны результаты расчетов остаточных напряжений в стержнях фермы (рис. 2).

 

Таблица 3- Остаточные напряжения после нагрузки силой P_T,AB=22522N и разгрузки. Силы с положительным знаком обозначают растяжение стержня фермы

Обозначение элемента	Упругое состояние	Состояние после пластической деформации в элементе CD [N]	Силы в элементах фермы после разгрузки [N]	Остаточные напряжения [МПа]
AB	-1.321P	-1.995P+14932	-247	-2.47
BC	0.961P	21213	-408	-4.08
CD	1.36P	30000	-584	-5.84
DA	-0.321P	-1.002P+15033	-305	-3.05
DB	0.718P	2.237P-33557	654	6.54
AC	-0.961P	21213	408	4.08

 

Из данных приведенных в таб. 3 видно, что после стержня CD пластическая деформация появится в стержне AB. Из уравнения (2) рассчитана сила при которой начнется пластическая деформация в стержне AB.

                      (2)

Силы в элементах после разгрузки рассчитаны соответственно с теоремой о разгрузке. Они равны разности между силами, возникшими в состоянии после пластической деформации в элементе CD и силами из упругого состояния для нагрузки силой P_T,AB=22522N. Нужно обратить внимание, что при нагрузке ферменной конструкции силой больше чем указанная P_T,AB конструкция превратится в механизм. После нагружения анализируемой конструкции силой P_T,AB и разгрузки, в ней появятся остаточные напряжения, указанные в таб. 3. Эти напряжения нужно взять в учет при дальнейших нагрузках конструкции, так как они приводят к понижению предела упругости в стержнях фермы.

 

Список использованных источников

1.      Биргер, И. А. Остаточные напряжения [Текст]/ И.А.Биргер. -М.: Государственное научно-техническое издательство машиностроительной литературы, 1963.

2.      P. J. Withers and H. K. D. H. Bhadeshia, “Residual stress Part 2 – Nature and origins”, Materials Science and Technology, Vol. 17, 2001. -366-375.