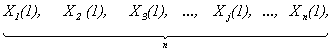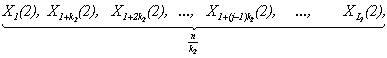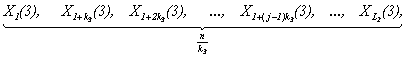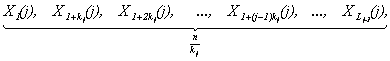ОПТИМИЗАЦИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ C ОГРАНИЧЕННЫМ ОБЪЕМОМ ИНВЕСТИРОВАНИЯ
INVESTMENT PORTFOLIO OPTIMIZATION WITH LIMITED INVESTMENT
Семенчин Е.А., Шаталова А. Ю. (КубГУ, г. Краснодар, РФ)
Semenchin E.A., Shatalovа A. Yu. (Kuban State University)
В [1, 2, 3] исследована задача максимизации дохода, получаемого предприятием за счет инвестирования m проектов без учета альтернативных источников инвестирования, предложена и описана методика ее решения.
В данной работе исследована задача с учетом дополнительных источников инвестирования.
In [1, 2, 3] described a method for maximizing profits derived by an enterprise through investment projects m without restrictions on the amount of alternative investment.
In this work the task taking into account additional sources of investment is investigated.
Ключевые слова: инвестиционный проект, инвестиционный портфель, инвестиционный фонд, объем инвестирования.
Key words: investment projects, investment portfolio, investment fund, investment level.
1. Постановка задачи
На предприятии рассматриваются m проектов, которые будут
инвестироваться в течении n (n 
2) месяцев с целью получения
прибыли.
Первоначальный объем инвестиционного капитала предприятия
составляет с рублей. Бюджет инвестиционного фонда будет пополняться предприятием
каждый i-ый (i=1, 2, …, n-1) месяц на сумму 
(
)
рублей (i= 2, …, n-1) за счет специально
выделяемых предприятием денежных средств. Сумма устанавливается
заранее. Пополнение инвестиционного фонда в моменты 
возможно также за счет
прибыли, получаемой от реализации каждого j-го инвестиционного
проекта, j=1, 2, …, m.
Предполагается, что предприятие может получать по t процентов в месяц за краткосрочный вклад в банк (альтернативный источник вложения денежных средств, которые не были проинвестированы в текущем месяце [4]). Существует также ограничение на объемы инвестирования рассматриваемых проектов: не более p рублей в месяц в каждый проект.
Периодичность инвестирования предприятием j-го проекта равна месяцам (j=1, 2, …, m), величина прибыли,
которую он ожидает получить от реализации j-го проекта, составляет 
процентов от размера
инвестируемой суммы, индекс риска для j-го проекта составляет 
(j =1, 2, …, m). В течение любого
месяца средний индекс риска инвестиционных проектов не превышает l (l=const), средняя
продолжительность инвестирования проектов не превышает r месяцев (r=const),
Цель данной работы – построить математическую модель, позволяющую максимизировать доход предприятия, который оно получит к концу n-го месяца от инвестирования всех рассматриваемых проектов с учетом указанных выше ограничений.
2. Оптимизация инвестиционного портфеля c ограниченным объемом инвестирования
Обозначим, как и в [1, 2, 3], через 
, 
,
, …, 
, …, 
– все возможные делители числа
n, =n (<<<<…<), где 
совпадает с периодом инвестирования предприятием j-го (j =1, 2, …, m) проекта. 
(α=1, 2, …,
(m-2)) – заключительный
момент инвестирования β-го (β=2, 3,…, (m-1)) проекта.
Кроме того (см. [1, 2, 3]), обозначим через 
– объем инвестирования в
инвестиционный проект j (
) в 
-ом месяце (
). В соответствии с [1, 2, 3]
для каждого j-го
проекта переменная в каждый момент v будет иметь вид:
|
для 1-го проекта –
для 2-го проекта –
для 3-го проекта –
…………………………………………………………………… для j -го проекта –
…………………………………………………………………. для m -го проекта –
|
(1)
|
где n, 
, 
, 
,
…, 
– число различных объемов
инвестирования в 
-ом месяце (=1, 2, …, n), через Хv(B) (=1, 2, …, n) – объемы денежных
средств, вложенных предприятием в дополнительный источник инвестирования.
Условие максимизации объема дохода, получаемого предприятием от реализации рассматриваемых инвестиционных проектов, будет иметь вид:
|
|
(2) |
Укажем ограничения, которым должны удовлетворять
объемы вложений 
(, j
). Согласно постановке
задачи (см. п.1), первоначальный объем инвестиционного капитала предприятия
составляет с рублей. Согласно этому условию объем всех денежных средств на
конец 1-ого месяца, инвестируемый в имеющиеся инвестиционные проекты, должен
быть равен этой сумме:
(3)
суммарный объем вложений в инвестиционные проекты на конец первого месяца.
Текущие инвестируемые средства в рассматриваемые
проекты в i-ом месяце будут равны
сумме специально выделенных предприятием денежных средств ( рублей (i=1, 2, …, n-1)) плюс прибыль,
полученная от реализации инвестиционных проектов (в том числе и альтернативных)
за предыдущий период времени:
=
–
объемы вложений на конец второго месяца;
…………………………………………..
=
–
(4)
объемы вложений на конец v-го месяца;
…………………………………………………………
=
–
объемы вложений на конец (n-1)-го месяца;
где 
– означает
суммирование по тем j (j=1, 2, …, m), для которых 
является делителем (v-1), т. е. суммируются только
те объемы вложений, которые уже вернулись прдприятию с учетом указанной
процентной ставки прибыли на текущий момент времени.
Очевидно,
|
…………..…………………………….
……………………………………..….
|
((5) |
В соответствии с п.2 имеем дополнительные ограничения:
|
|
(6) |
где 
Соотношения (2)-(6) представляют собой математическую модель максимизации дохода, получаемого предприятием за счет реализации рассматриваемых инвестиционных проектов при учете альтернативных источников инвестирования.
3. Пример
В компании рассматривается 4 проекта с целью их инвестирования в течение n=6 месяцев и получении от них за счет этого максимального дохода.
Первоначальный объем инвестиционного капитала банка составляет 500 000 рублей. Бюджет инвестиционного фонда будет пополняться банком в 4-ом месяце на сумму 250 000 рублей за счет специально выделяемых предприятием денежных средств (пополнения инвестиционного фонда вначале 1-го, 2-го, 3-го, 5-го месяцев за счет дополнительных денежных средств равны нулю). Кроме того, пополнение инвестиционного фонда будет осуществляться в каждом месяце за счет дохода, получаемого от реализации этих же инвестиционных проектов, т. к. наименьший период инвестирования равен одному месяцу [1, 2, 3]. Периоды инвестирования рассматриваемых четырех инвестиционных проектов (№1, №2, №3, №4,) равны соответственно 1, 2, 3 и 6 месяцам; проценты прибыли проектов равны соответственно 5; 7; 9; 11 ежемесячно от инвестируемой суммы; индексы рисков составляют соответственно 1, 4, 9, 7. Средний индекс риска для всех проектов не превышает 6, средняя продолжительность инвестирования проектов не превышает 2,5 месяца [1, 2, 3]. Кроме того в компании предполагают получать дополнительную прибыль в размере 5% в месяц за краткосрочный вклад в банк тех денежных средств, которые не были вложены в инвестиционные проекты в данном месяце.
При указанных способах и утвержденном графике инвестирования проектов необходимо найти максимальный доход, который предприятие может получить по окончанию реализации этих проектов.
Воспользовавшись математической моделью (2)-(6) и методикой анализа подобных моделей [5], найдем решение данной задачи:
|
F=885473,8,
|
(7) |
Таким образом, максимальный доход, который может получить предприятие после реализации рассматриваемых проектов, составляет 1885473 рубля, а объемы инвестирования в рассматриваемые моменты времени определяются равенствами (7).
Список использованных источников
1. Семенчин Е. А., Шаталова А. Ю. Обобщенная математическая модель инвестирования предприятий с учетом рисков // Фундаментальные исследования. Экономические науки. -2011. -№ 13 (часть 1).
2. Семенчин Е. А., Шаталова А. Ю. Математическая модель максимизации прибыли, получаемой банком за счет реализации инвестиционных проектов // Фундаментальные исследования. Экономические науки. -2012.- № 6.
3. Семенчин Е. А., Шаталова А. Ю. Инвестиционный портфель с переменным объемом фонда инвестирования // Фундаментальные исследования. Экономические науки. -2012.- № 9.
4. Хачатрян С.Р., Пинешня М.В., Буянов В. П. Методы и модели решения экономических задач. -М., 2005.
5. Шаталова А. Ю. Методика решения обобщенной математической модели инвестирования предприятий с учетом рисков // Научный электронный архив. URL: http://econf.rae.ru/article/6521 (дата обращения: 30.01.2012).