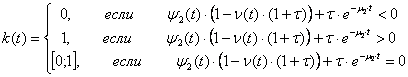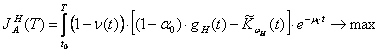МОДЕЛЬ ОЦЕНКИ ЭФФЕКТОВ СИНЕРГИИ ДЛЯ ПРЕДПРИЯТИЙ-УЧАСТНИКОВ ПРОИЗВОДСТВЕННОЙ КОРПОРАТИВНОЙ ГРУППЫ

 

MODEL OF SYNERGY EFFECTS ESTIMATION FOR PARTICIPANTS OF PRODUCTION CORPORATE GROUP

 

Дученко Д.В. (ЧГУ, г.Череповец, РФ)

Duchenko D.V. (The Cherepovets state university)

 

Рассмотрена корпоративная структура, состоящая из предприятия-производителя и потребителя-кредитора. Определяется оптимальная программа совместного инвестирования производителя корпоративной продукции. Проводится оценка и иллюстрация эффектов синергии.

We consider the corporate structure consisting of the manufacturing entity and the consumer-creditor. We determine the optimum program of joint investment of the producer of corporate products. The assessment of effects of a synergy is carried out.

 

Ключевые слова: корпоративная структура, интеграция, эффект синергии, корпоративные цены, кредитно-акционерные связи.

Key words: corporate structure, integration, effect of a synergy, corporate prices, credit and joint-stock communications.

 

В условиях рыночной экономики важна правильная организация инвестиционного процесса на уровне хозяйствующего субъекта производственной корпоративной структуры. Основной смысл вертикальной интеграции заключается в реализации синергетических возможностей путем сокращения прямых издержек на составляющих производства и снижении цен на товары и кредиты внутри группы.

Большое распространение получили модели оценки эффективности предприятий в  рамках  вертикальных  образований [2,4]. В процессе управления эффективностью ФПГ применяются статистические методы [1]. Проблема оптимизации структуры финансово-кредитного механизма ФПГ, сводящаяся к установлению требуемых соотношений между его отдельными компонентами, решается в [3]. Роль финансово-промышленных групп в оптимизации финансовых потоков отмечена в [5].

В [4]  подробно проведен детальный экономический анализ взаимодействия предприятий, являющихся участниками  финансово-промышленной группы. Но менее подробно автор [4]  исследует производственную корпоративную группу, обладающую некоторыми особенностями (функции кредитора выполняет не банк, а предприятие-потребитель корпоративной продукции). И в том и другом случае, для получения оптимальной инвестиционной программы, определяются оптимальные на заданном интервале этапы совместного инвестирования производителя, доставляющего участникам группы максимальные гарантированные доходы. Для определения результатов автор предлагает решать последовательно на каждом интервале краевую задачу с соответствующими граничными условиями. Окончательное аналитическое решение предлагается получить с использованием приближенных методов, что вносит некоторую погрешность: определяется близкая к оптимальной программа совместного инвестирования производителя.

В настоящей работе предложен подход, отличающийся  от [4] тем, что исследование поведения игроков проводится на всем планируемом интервале. Решение оптимизационных задач проведено с использованием принципа максимума Понтрягина, предоставляющего необходимые условия оптимальности динамического процесса при наличии ограничений на управление. Для решения вариационных задач использован метод Рунге-Кутты 4-го порядка. Предложенный механизм инвестиционной стратегии позволяет более полно определить объем финансовых ресурсов и использовать оптимальные формы привлечения инвестиций.

В разделе 1 приводится решение оптимизационных задач для предприятия-производителя продукции и потребителя-кредитора для случая участия в  корпоративном объединении. В разделе 2 рассматривается решение аналогичных задач для случая независимой деятельности. В разделе 3 представлены численные результаты. Непосредственно на модели определяются оптимальные значения корпоративных цен. Вычисляются интеграционные эффекты, получаемые участниками при объединении в корпоративную группу, приводится иллюстрация эффектов синергии.

 

1.     МОДЕЛЬ ПРОИЗВОДСТВЕННОЙ КОРПОРАТИВНОЙ ГРУППЫ

Механизм вертикальной интеграции возникает при сочетании владения потребителем-кредитором (предприятие ) частью собственности производителя (предприятие ) и кредитованием производителя  с целью снижения его производственных затрат. В такой ситуации возникают противоречивые интересы, так как каждый участник преследует свои собственные цели. Для разрешения подобных противоречий примениʹм аппарат теории игр.

Мы не предполагаем проводить описание основных характеристик деятельности участников, а также структуру финансовых потоков. Подробно математическое описание модели подобной корпоративной структуры дано в [4]. В настоящей статье хотелось бы уделить особе внимание рассмотрению возможности оценки максимальных гарантированных доходов участников, получаемых ими на протяжении всего планируемого периода .

Рассматривается задача выбора оптимальных управлений потребителя-кредитора  и производителя  на заданном интервале планирования, обеспечивающих достижение в конце интервала максимальных значений критериев  и . В качестве фазовой координаты используется ресурс  производителя; ,  –  управление потребителя-кредитора (кредит, выдаваемый  в период ),  – управление   (собственные отчисления от прибыли в период ). Динамика процесса описывается уравнением  с начальным условием:  . Оптимальные управления игроков отыскиваются в классе кусочно-непрерывных программных управлений. 

 

Оптимизационная задача для производителя (предприятие А)

Предприятие-производитель решает свою оптимизационную задачу при известной ему стратегии потребителя-кредитора  на интервале . Предприятие   должно так распорядиться собственными средствами  при , чтобы максимизировать свой интегральный доход :

1.     Критерии предприятия А: .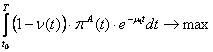                                                                         

2.     Уравнение динамики состояния системы: , .

3.     Начальное условие фазовой траектории:  .                          

4.     Ограничение на управление: .

Гамильтониан: , лагранжиан: . Таким образом, с учетом необходимых условий оптимальности:

1)     Уравнение Эйлера:

2)     Условие трансверсальности:  

3)     Принцип максимума:

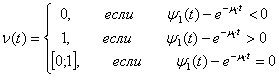
4)     Неотрицательность множителей Лагранжа:.

Таким образом, краевая задача принципа максимума для  (при совместной деятельности) принимает вид:

	(1.1)

При задании начального условия  для различных фиксированных значений параметра  получаем семейство параметрических траекторий, обеспечивающих для различных  максимумы критерия  и удовлетворяющих заданному начальному условию. Для выбора из этого множества единственной траектории, обеспечивающей достижение максимального значения критерия предприятия-потребителя, необходимо далее искать его оптимальное управление на интервале  с учетом полученных для  результатов.

 

Задача выбора оптимального управления потребителя-кредитора В

Поведение предприятия  в рассматриваемой игровой ситуации является более сложным, чем поведение производителя , так как потребитель-кредитор имеет возможность влиять на управление системой, воздействуя на производителя , акциями которого он обладает. Предполагается, что  обладает  достаточной информацией о производственных характеристиках производителя А.

Определим оптимальное управление потребителя-кредитора (с учетом управлений  производителя), доставляющее максимум критерию , представляющему собой интегральное значение гарантированной прибыли предприятия  на интервале:

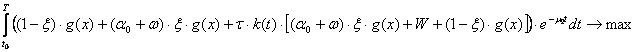
Рассуждая так же, как и в  случае с задачей производителя , с учетом необходимых условий оптимальности для оптимизационной задачи потребителя-кредитора составили следующую краевую задачу принципа максимума:

	(1.2)

Полученные выражения определяют для участников группы максимальные гарантированные доходы на планируемом интервале их деятельности, которые они могут получить при выполнении совместной программы. Для окончательного определения результатов на интервале  необходимо решить краевую задачу с соответствующими граничными условиями. Описанная структура будет эффективной лишь в том случае, если существование группы экономически более выгодно каждому участнику, чем независимая деятельность каждого из них.

 

2.     ИССЛЕДОВАНИЕ МОДЕЛИ КОРПОРАТИВНОЙ ГРУППЫ

Обозначим критерии получения максимальных гарантированных доходов при независимой деятельности производителя  и предприятия  за тот же период  соответственно через , . Объединение предприятий в  производственную корпоративную структуру целесообразно, если существуют такие условия, при которых суммарный за период  максимальный гарантированный результат для каждого участника превышает его аналогичный результат, полученный при независимой деятельности: , . При независимой деятельности предприятий информативность участников не обеспечивается, и прежде всего, предприятие  не имеет информации о структуре удельных затрат производителя.

 

Оптимизационная задача для предприятия-потребителя В

Считаем, что В приобретает всю продукцию у , но теперь уже по рыночной цене . Так как непосредственно от купли-продажи прибыль предприятия  равна нулю, то прибыть потребителя в момент  складывается из  за кредит  и доли  участия в акционерном капитале предприятия .

Теперь возможные доходы предприятия  от этих двух операций независимы. Поэтому потребителю  выгоднее всего вкладывать свои средства и на весь период в тот источник дохода, который дает большую прибыль: . Здесь  - % за кредит, выплачиваемый предприятием ,  – доли дохода , причитающиеся по акциям предприятию .

Критерий предприятия потребителя при независимой деятельности:

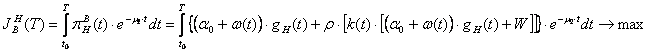
С учетом необходимых условий оптимальности для потребителя-кредитора краевая задача принципа максимума при независимой деятельности:

(2.1)

 

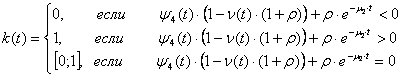
Оптимизационная задача для предприятия- производителя А

С учетом стратегии кредитования предприятия  производитель  распоряжается своими средствами  так, чтобы максимизировать свой интегральный доход:                                                          

(2.2)

Таким образом, краевая задача для А при независимой деятельности:

(2.3)

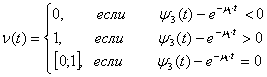
Для определения максимальных гарантированных результатов независимой деятельности необходимо решить краевую задачу (3.9) с соответствующими граничными условиями на всем интервале .

 

3.     ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ МОДЕЛИ КОРПОРАТИВНОЙ ГРУППЫ

Для определения условий, при выполнении которых согласованная деятельность предприятий является экономически более эффективной, провели сравнительный анализ результатов совместной и независимой деятельности участников группы.

Для различных комбинаций параметров, характеризующих внутрикорпоративные цены, получили множество оценок интегральных доходов участников группы. Из полученного множества оценок отыскали  оптимальную точку , которой соответствуют значения целевых функционалов игроков, превышающие аналогичные результаты их независимой деятельности. Для этого свели двухкритериальную задачу к однокритериальной задаче, целевая функция которой представляет весовую комбинацию исходных критериев: .

Решение  является Парето-оптимальным, если для всех  выполняется условие , или

Итак, для нашей задачи , что соответствует оптимальным значениям . Внутрикорпоративная ставка по кредиту составит . Внутренняя трансфертная цена на продукцию с учетом :  руб. При данных корпоративных ценах эффект от интеграции будет положительным для обоих участников:

 руб.

 руб.

Иллюстрация так называемого интеграционного эффекта (или эффекта синергии), получаемого участниками в случае объединения в корпоративную структуру, приведена ниже [Рисунок 1, 2].

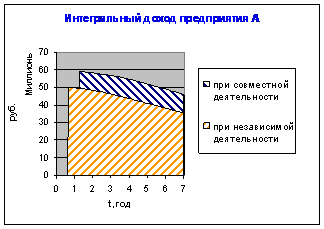
Рисунок 1 – Иллюстрация эффекта синергии для предприятия А

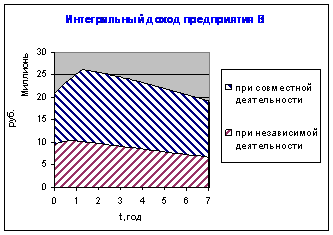
Рисунок 2 – Иллюстрация эффекта синергии для предприятия В

 

Использовано одно из свойств определенного интеграла от неотрицательной функции, который с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком подынтегральной функции , слева и справа – прямыми  и , снизу – отрезком оси абсцисс. В наших обозначениях интегральный доход представлен в ви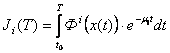де: ,  где   –  накапливаемый доход i-предприятия. Интеграционный эффект можно определить вычитанием площадей соответствующих фигур.

Модель автоматизирована посредством объединения макросов (VBA) с последовательностью выполнения операций. Существенной особенностью модели является то, что она позволяет пользователю, не вникая в зависимости и сложный математический аппарат, получать результаты моделирования, выполняя заданную последовательность действий. Среди основных свойств модели можно отметить гибкость, позволяющую легко вносить изменения в начальные данные, что создает возможность для проведения различных сценариев. Так, кроме определения оптимальных параметров , обуславливающих экономическую целесообразность корпоративного объединения, модель позволяет определить некоторые другие начальные параметры, доставляющие больший выигрыш от данного взаимодействия (например,  – начальную долю владения акциями производителя).

Проведенные модельные эксперименты показывают, что изменение корпоративных цен влияет не только на значения интегральных доходов, но и оказывает влияние на саму программу инвестирования; при некоторых значениях корпоративных параметров рассчитанный интегральный доход может получаться отрицательным.

 

ЗАКЛЮЧЕНИЕ

Таким образом, в результате исследования экономической эффективности производственной корпоративной структуры определили оптимальную программу совместного инвестирования производителя участниками группы на протяжении всего планируемого интервала . В результате согласованной деятельности каждый из участников получит максимальные гарантированные результаты, которые будут превышать аналогичные результаты их независимой деятельности. Полученные численные результаты подтверждают, что такая модель оптимизации отношений между покупателем и продавцом может быть вполне адекватной при оценке целесообразности инвестирования в новую технологию производства.  

Список использованных источников

1.      Бандурин В.В. Корпоративное управление в условиях рынка: Мон. / Бандурин В.В., Беленький Л.П., Блинов В.В.;. – М.: Министерство обороны РФ, 1996. – 125 с.

2.      Додонова А.Р. Создание финансово-промышленных групп. Модель сигналов / Препринт BSP/98/007 – М.: РЭШ, 1998. – 25 с.

3.      Коняев А.А. Финансово-кредитный механизм функционирования финансово-промышленных групп России: Автореф. дис. канд. экон. наук. – Саратов: СГСЭУ, 2007.

4.      Косачев Ю.В. Экономико-математические модели эффективности финансово-промышленных структур. – М.: Логос, 2004. – 248 с.

5.      Орехов С.А. Менеджмент финансово-промышленных групп: Учеб. пособие / Орехов С.А., Селезнев В.А. – М.: МЭСИ, 2005. – 176 с.

6.      Плещинский А.А. Эффективные схемы межфирменных взаимодействий: механизм равновесных трансфертных цен / Препринт. – М.: ЦЭМИ РАН, 2000. – 90 с.