моделирование сил резания и характеристик съема припуска при двустороннем шлифовании торцов одиночной  заготовки

 

Вайнер Л.Г. (ТОГУ, г.Хабаровск, РФ)

 

Method was worked out for determination of technological parameters such as stock allowance assignment, variation of work removal parameter, cutting forces, elastic deformation along the trajectory  of  the blank  supply movement at double-disc grinding .

 

В настоящее время среди многообразия схем двусторонней торцешлифовальной обработки распространены и схемы шлифования одиночных заготовок (с круговым поступательным или возвратно-поступательным движением подачи).

Реальная геометрическая форма технологического пространства, в котором перемещаются обрабатываемые заготовки, определяет условия физико-механического взаимодействия инструментов и заготовки, характер съема припуска при движении заготовок вдоль траектории подачи и, соответственно, структуру цикла шлифования, силы резания, под действием которых происходят упругие смещения шлифовальных кругов (ШК), которые, в свою очередь, ведут к изменению реальной формы технологического пространства.

Данная работа посвящена методологическим аспектам определения характеристик съема припуска, сил резания и упругих смещений на примере шлифования одиночной заготовки с круговой траекторией подачи. Отметим, что все положения предложенного расчетного метода справедливы и для прямолинейной траектории подачи заготовки. Обозначим: R_Д - радиус окружности расположения осей заготовок, R_К - наружный радиус ШК, а – межосевое расстояние, ω_Д и ω_К – угловые скорости вращения устройства подачи и ШК, V_Д – скорость подачи заготовки, φ_i  - текущая угловая координата заготовки в i-й точке траектории.

Основной геометрической характеристикой технологического пространства служит кривая формы технологического пространства - КФТП – кривая, образованная при пересечении производящей торцовой поверхности ШК и так называемой поверхности подачи заготовок - поверхности, образованной перемещением прямой линии - оси заготовки вдоль траектории движения подачи заготовок.

Необходимо различать начальную КФТП_Н (без нагрузки – «при шлифовании воздуха») и реальную КФТП (при нагружении ШК силами резания) [1].

КФТП_Н определяет эквивалентное врезное перемещение – относительное сближение производящей поверхности ШК и обрабатываемой поверхности в направлении нормали к обрабатываемой поверхности при перемещении заготовки вдоль траектории движения подачи.

При рассмотрении цикла шлифования одиночной заготовки представляется возможным использовать аналогию этого процесса с круглым врезным шлифованием. В обоих случаях имеются этапы активного съема и снятия натяга (выхаживания). Отличие состоит в том, что в случае круглого врезного шлифования управляющим воздействием служит изменение номинальной врезной подачи [2], а при двустороннем торцешлифовании – номинальный закон текущего сближения ШК и заготовки, определяемый КФТП_Н.

Фактический съем материала заготовки (или текущий снимаемый припуск) t(θ) (отличается от номинального t_Н(θ) на величину упругих деформаций системы под заготовкой Δ.

   ,                                              (1)

здесь θ – текущая угловая координата заготовки, считая от входа в зону шлифования.

Поскольку координаты точки приложения силы резания, действующей на ШК, в случае обработки одиночной заготовки совпадают с ее координатами в зоне шлифования, упругое смещение системы под заготовкой

,                                                    (2)

здесь:

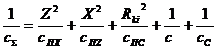                                       (3)

- приведенная суммарная податливость системы под заготовкой; с_Σ – приведенная суммарная жесткость системы под заготовкой; с_ПХ  и с_ПY – приведенные поворотные жесткости планшайбы относительно осей X и Y, соответственно; с_ПС – приведенная поворотная жесткость стыка ШК-планшайба;  с  и с_С – приведенная осевая жесткость планшайбы и стыка ШК-планшайба, соответственно; R_Ki – текущий радиус расположения заготовки.

Нормальная сила резания P_Y определяется на основе классической теории шлифования из энергетических соотношений [3]. Для круговой траектории

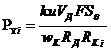 ,                                                   (4)

здесь k - соотношение нормальной и тангенциальной составляющих сил резания, u – удельная энергия шлифования,  F – площадь обрабатываемого торца заготовки,

                                                                       (5)

- скорость съема припуска.

После подстановки (2) в (1) с учетом (4) и (5) получаем дифференциальное уравнение съема припуска

 ,                                                  (6)

где

,                                                  (7)

заметим, что  с_Σ и R_Ki зависят от текущей угловой координаты θ.

Уравнение (6) является линейным дифференциальным уравнением с общим решением [4] в виде

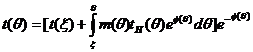,                                 (8)

здесь t(ξ), ξ – координаты точки, через которую проходит интегральная кривая,

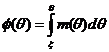.                                                  (9)

Для возможности решения данного уравнения в явном виде введем ряд допущений.

1. Анализ работ по исследованию и практическому применению процесса двусторонней торцешлифовальной обработки показывает, что производящая торцовая поверхность ШК может иметь плоскую, коническую или параболическую форму. В большинстве случаев начальную КФТП_Н можно аппроксимировать многочленом второй степени (что подтверждается результатами экспериментальной оценки формы зоны шлифования [1])

.                                             (10)

Коэффициенты многочлена определяются из условий: 1) при θ=0 t_Нa=0; 2) при θ= θ_mн  t_Нa=0,5Δt_Н (Δt_Н – перепад КФТП_Н, θ_mн – угловая координата экстремума КФТП_Н); 3) при θ=θ_mн   .

2. Разделим зону шлифования на n интервалов величиной 2φ_в/n (рис. 1), в пределах каждого из которых можно принять m(θ)=const.

 

 

 

 

 

 

 

 

 

 

 

 

 

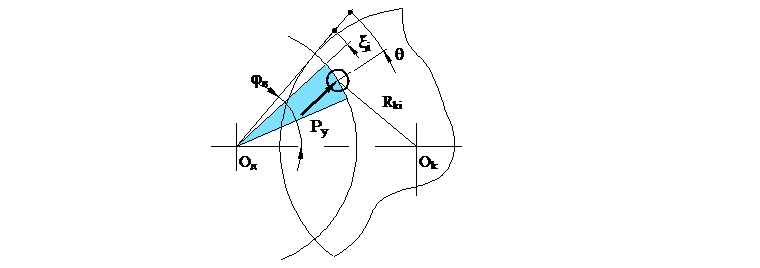
Рисунок 1- К расчету характеристик съема припуска

 

Координаты заготовки X, Z, R_ki и приведенная суммарная жесткость системы под заготовкой с_Σ  определяются для центральной точки интервала. Тогда для i-го интервала m(θ) определяется из выражения (7) при

с_Σ= с_Σi,

,

,

,

,

,

.

Полагая t_Н(θ)= t_Нa(θ), получим выражения для текущего съема t(θ) и скорости съема   припуска на участке активного съема при 0≤ θ ≤ θ_mн

,               (11)

,                            (12)

где a₃=a₁-2a₂/m.

На участке выхаживания при θ>θ_mн процесс съема припуска продолжается за счет имеющегося натяга в системе

.

Тогда с учетом начальных условий – при θ=θ_mн t=t(θ_mн) на этапе снятия натяга

,                              (13)

.                                                  (14)

Нормальная сила резания определяется при подстановке (12) и (14) в выражение (4). Тангенциальная составляющая силы резания P_τ=P_y/k.

Суммарные упругие смещения ШК под заготовкой в произвольных точках траектории ее движения определяются по известным силе резания и приведенной жесткости с помощью выражения (2).

Корректность предложенной методики подтверждена сопоставлением расчетных и экспериментальных кривых распределения нормальных сил резания, действующих на заготовку, вдоль траектории ее движения. Методика и условия эксперимента описаны в работе [1]. 

На основе приведенной методики и расчетных зависимостей создан алгоритм и программа, позволяющие проанализировать влияние технологических параметров на характеристики съема припуска и силы резания, что может быть использовано для управления процессом ДТШО.

 

Литература

1. Моделирование технологических процессов абразивной обработки. Монография. / Г.В. Барсуков, Л.Г. Вайнер, Ю.В. Василенко и др.; Под ред. Ю.С. Степанова и А.В. Киричека -  М.: Издательский дом «Спектр», 2011. -  252 с.

2. Михелькевич В.Н. Автоматическое управление шлифованием. – М.: Машиностроение, 1975. – 304 с.

3. Лурье Г.Б. Шлифование металлов. / Г.Б. Лурье.– М., Машиностроение, 1969.– 172 с.

4. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука, 1980. – 976 с.