Анализ распределения азота на фазовых границах азотированного слоя
Крукович М.Г. (МИИТ, г. Москва, РФ),
Бадерко Е.А. (МГУ, г. Москва, РФ),
Клочков Н.П. (МИИТ, г. Москва, РФ)
In work the analysis of the distribution of nitrogen in the nitrided layers on the boundary of phases and the possibility of accounting for variable coefficient diffusion on each border.
Важным
этапом моделирования процесса формирования азотированного слоя является учет
распределения азота на фазовых границах. Впервые
уравнение для скорости перемещения межфазной границы было предложено Вагнером. Для
решения задач многофазной диффузии в моделях [1, 2] принимается, что движение
межфазных границ 
описывается уравнением
Стефана, определяющим условие баланса вещества при фазовых переходах (рис. 1):
,
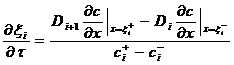(1)
где 
- скорость движения
i-той границы; 
- коэффициент диффузии азота в
i-той фазе; 
- предельные растворимости
азота в фазах (слева (-) и справа (+) от i границы), определяются по диаграмме
состояния и могут изменяться со временем при изменении температуры; i=1, 2,
...., m.
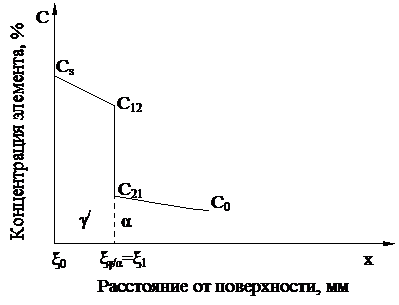
Рисунок 1 - Схема перемещения межфазных границ при азотировании [2]
Построение модели на основе предположения о том, что в начальный момент азотированный слой имеет очень тонкие толщины по сравнению со значениями общей толщины слоя, полученной после азотирования, не отвечает реальному процессу. Расчет предполагает необходимость произвольного постулирования начального распределения фаз, в то время как это распределение должно быть получено как следствие взаимодействия компонентов, определяемое уравнением диффузии и граничными условиями.
Движение границы в этом случае описывается диффузионной моделью, используемой при внешнем окислении металлов. Толщина слоя (е) в этом случае определяется по формуле [6]:
,
(2)
где r - отношение между азотом и металлом в образующемся нитриде;
[N]α - концентрация азота на поверхности α – твердого раствора;
М – атомная концентрация металла в образующемся нитриде;
- коэффициент диффузии азота в железе при
соответствующей температуре обработки;
t – продолжительность обработки.
Попытка описать распределение азота непрерывной функцией на основе выбора среднего значения коэффициента диффузии, более или менее соответствующей его изменению при понижении концентрации азота, в зависимости от координаты в многофазном слое [3, 4, 5] не привела к получению приемлемых результатов. При переходе межфазной границы концентрация изменялась плавно непрерывным образом, что не соответствует экспериментально наблюдаемому распределению. На кривой распределения азота по глубине слоя существует ступенька, т.е. в межфазной переходной зоне значение концентраций скачкообразно изменяется от значения С1, соответствующего диаграмме состояния Fe-N до значения С2.
Аналитическое
решение уравнений диффузии и использование метода Матано при рассмотрении
кинетики роста фаз азотированного слоя на железе показало, что рост фаз азотированного
слоя подчиняется параболическому закону: 
.
Полученные системы уравнений, включающие коэффициент массопереноса, оказались нелинейными. Они решались итерационным способом для каждой фазы слоя (рис. 2). Метод Матано по существу является графическим и ошибка при его применении резко увеличивается на концах концентрационной кривой, что впоследствии приводит к большим ошибкам расчетных значений.
Развитие концентрационного профиля по толщине фаз слоя (ε, γI, α) рассчитывали по результатам решения второго уравнения Фика и баланса сохранения масс. При этом граница представляется в виде слоя некоторой толщины с аккумулированным содержанием азота, обеспечивающим локальное термодинамическое равновесие на границе. Получены следующие расчетные формулы.
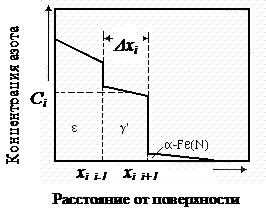
Рисунок 2 - Схематическое изображение трехфазного азотированного слоя
На границе ε/γI формула имеет вид:
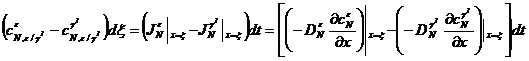. (3)
На границе γI/α формула имеет вид:
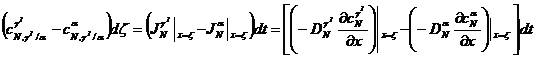. (4)
Расчет проводится для каждой границы отдельно.
Проблема, затрудняющая решение многофазной диффузионной задачи, является следствием изменения коэффициента диффузии при переходе межфазной границы. На микроструктурном уровне подобное изменение представляется скачком. Не вызывает сомнений допустимость представления о постоянстве значения коэффициента диффузии в пределах фазы. Однако также является очевидным, что при переходе межфазной границы коэффициент диффузии изменяется от значения, соответствующего коэффициенту диффузии в одной фазе до значения в другой. Игнорирование этого изменения нарушает баланс вещества в окрестности точки, соответствующей межфазной границе. Для сохранения баланса вещества необходимо вычислить производную коэффициента диффузии по концентрации.
Для преодоления общей сложности необходимо уточнить физические представления о характере переходной зоны в окрестности межфазной границы. Очевидно, что межфазная граница не является идеально плоской и занимает некоторый объем. Уже на микроструктурном уровне при большом увеличении отчетливо просматриваются неровности, ступенчатость, обусловленная различной скоростью роста фазы в различных местах фронта диффузии. Таким образом, если выделить окрестность диффузионной зоны вблизи межфазной границы, её можно представить в виде слоя некоторой толщины. Из этого следует, что при переходе межфазной границы значение коэффициента диффузии может изменяться непрерывным образом от значения, соответствующего коэффициенту диффузии в одной фазе до значения в другой. Согласно трактовке [6] в переходной зоне коэффициент диффузии принимает промежуточное значение.
Для описания изменения значения коэффициента диффузии в окрестности межфазной границы целесообразно использовать аппроксимирующую монотонную функцию, обеспечивающую плавный переход значений коэффициентов диффузии в области концентраций от С1 до С2. Но при этом вне перехода эта функция должна сохранять значения коэффициентов диффузии, свойственные фазам. Это должна быть функция со свойствами переключателя, но с плавным дифференцируемым переходом в промежуточной области значений концентраций. В качестве основы такой функции предложено использовать функцию Харрингтона, которая применяется в математической теории оптимизации для определения желательности того или иного фактора. В данном случае важна лишь ее способность задавать плавный переход между определенными значениями функции. В своем первоначальном виде эта функция представлена выражением:
(5)
где Y – значение функции; d – значения формального аргумента.
Рассматриваемая задача относится к классу задач с переменным коэффициентом диффузии. Для вычисления концентрации на любом шаге процедуры расчета необходимо задать значение производной этого коэффициента по концентрации или координате. А это зависит от понимания строения границы и интерпретации этого строения в модели. Первое, что приходит в качестве гипотезы – это попытаться описать скачкообразное изменение коэффициента диффузии в зависимости от концентрации. Скачкообразному распределению концентрации в слое будет соответствовать такая же зависимость коэффициента диффузии от расстояния от поверхности (рис. 3).
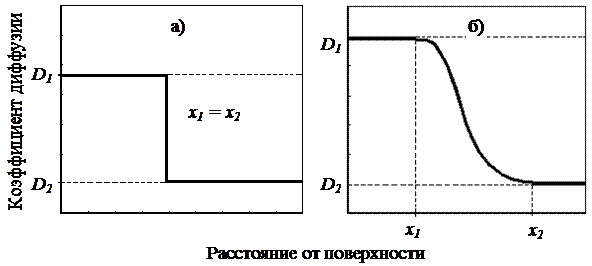
Рисунок 3 - Схема изменения коэффициента диффузии.
Если на графике (рис. 3 а) имеет место геометрический скачок, то на зависимости плавного изменения коэффициента диффузии от расстояния (рис. 3 б) имеет место область гомогенности. Эта область достаточно протяженна и для каждой системы протяженность ее соответствует своей системе. Коэффициент диффузии в этом случае изменяется достаточно быстро, но по существу декларирует модель, в которой физическое строение границы соответствует переходу одной кристаллической решетки к другой. Значение коэффициента диффузии при этом изменяется от D1 до D2.
Изменение коэффициента диффузии на границе раздела от концентрации насыщающего элемента в фазах также будет иметь плавный характер (рис. 4).
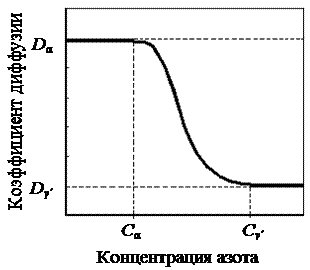
Рисунок 4 - Схема непрерывного изменения значения коэффициента диффузии в зависимости от концентрации азота в фазах
Для описания концентрационной зависимости коэффициента диффузии использована модифицированная функция Харрингтона. В данном случае важна лишь ее способность задавать плавный переход между определенными значениями функции. Она имеет вид:
(6)
где А - коэффициент усиления, отвечающий за значение верхнего приближения; X - значения аргумента функции; K - коэффициент усиления, определяющий протяженность переходной области по значениям параметра X; B - коэффициент смещения переходной области по значениям параметра X.
Было проведено тестирование функции. График распределения значений функции желательности Харрингтона, базирующийся на условных коэффициентах и условной области определения. Варьирование значениями коэффициентов в уравнении приводит к соответствующим изменениям значений функции. Таким образом, функция Харрингтона является легко управляемой посредством варьирования значениями коэффициентов A, B и K.
Вид кривых, построенных в соответствии с формулой (6) носит возрастающий характере. Для того чтобы зависимость была убывающей, в соответствии с требованиями (Рис. 3), функция Харрингтона была приведена к виду:
, (7)
Полученные результаты нового тестирования функции распределения представлены на рис. 5. При этом возможность управления полностью сохраняется и не отличается от управления возрастающей функцией.
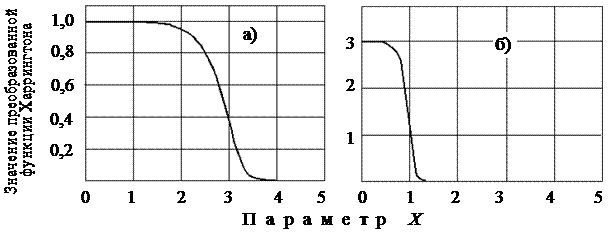
Рисунок 5 - Распределение значений преобразованной функции Харрингтона при различных значениях коэффициентов: а) A = 1, K = 3 и B = 2; б) A = 3, K = 10 и B = 1
В такой форме представления функции отсутствует возможность определения значения для нижнего приближения: оно всегда равняется нулю. Проведенное повторное модифицирование функции позволило задавать пределы области определения. В результате детального анализа была получена формула, в которой задаются граничные значения функции. Она имеет вид:
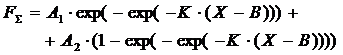, (8)
где А1 и А2 – коэффициенты усиления, отвечающие за значения границ приближений;
X – значения аргумента функции;
K – коэффициент усиления, определяющий протяженность переходной области по значениям параметра X;
B – коэффициент смещения переходной области по значениям параметра X.
Вид кривой, показанный на рисунке 6, получился в результате сложения двух модифицированных функций Харрингтона F1 в соответствии с формулой (6) и F2 в соответствии с формулой (7). Значение параметра А для F1 равно 1, для F2 – 2, коэффициенты К = 3 и В = 2 для обеих формул.
Если существует необходимость определения убывающей зависимости, то необходимо выполнение условия A1 < A2, а если возрастающей – то A1 > A2.
В результате была получена формула (9), с помощью которой можно задавать зависимость изменения коэффициента диффузии от концентрации на участке перехода через межфазную область.
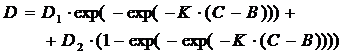(9)
где D1 и D2 – значения коэффициентов диффузии в фазе и в твердом растворе, C – текущее значение концентрации, K и B – соответственно, функциональные коэффициенты степени сжатия и сдвига предполагаемой межфазной области.
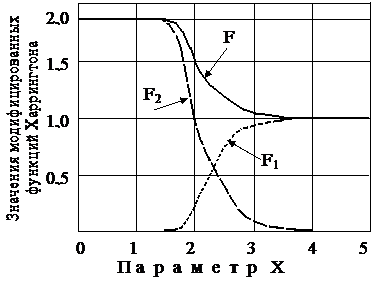
Рисунок 6- Графическое тестирование формулы (9)
Зависимость (9) была подвергнута тестированию при реальных значениях коэффициентов диффузии D1 и D2 , которые были равны 1,4·10 –11 и 1,9·10 –11 см 2/с, соответственно. Значения равновесных концентраций в данном случае для фазы составляло 0,8 % по массе, а для твердого раствора – 0,4 % по массе. Коэффициенты в формуле (9) К = 20,2 , В = 0,49 (Рис. 7). Таким образом, задается закон изменения коэффициента диффузии плавно меняющегося в зависимости от концентрации на участке возможного существования межфазной области. Однако, процесс установления нужных значений К и В достаточно долог, так как осуществляется путем подбора, ориентированного лишь на графической подгонке кривой под заданные значения равновесных концентраций. Возникает проблема оптимизации процедуры установления зависимости. Решением ее будет являться возможность непосредственного указания интервала аргумента с автоматическим вычислением реальных коэффициентов (К и В) уравнения (9). Для этого необходимо решить обратную задачу, а именно: на основании данных, полученных в результате многофакторного регрессионного анализа, установить зависимость каждого из коэффициентов К и В от значений равновесных концентраций С1 и С2.
В результате анализа были получены следующие формулы для расчета:
(10)
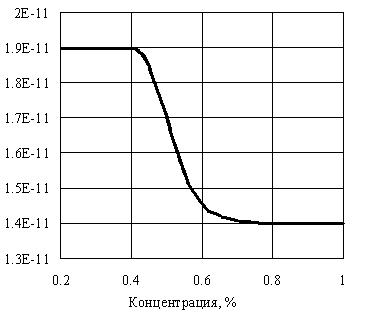
Рисунок 7- Зависимость коэффициента диффузии от концентрации на участке возможной межфазной области
Функция, как было предопределено, имеет область гомогенности в интервале концентрации между С1 и С2, что отражает возможность существования на этом промежутке межфазной области.
Таким образом, функция позволяет моделировать фазовую границу, как при плавном изменении коэффициента диффузии, так и при достаточно резком ее изменении. Подобная функция может также использоваться и при моделировании других зависимостей имеющих резкие изменения. Например, наблюдается достаточно резкий перепад твердости от слоя α-твердого раствора к твердости сердцевины на высоколегированных сталях после азотирования.
Литература
1. Лахтин Ю.М., Коган Я.Д., Шпис Х.-Й., Бемер З. Теория и технология азотирования. - М.: Металлургия, 1991, - 320 с.
2. Hickl A.Y., Heckel R.W. Kinetics of phase layer growth during aluminide coating of nickel // Metallurgical transactions. 1975, V. 6A. - P. 431-440.
3. Xia Lifang, Yan Mufu. Investigation of the mathematical model of the ion- nitrided layer growth // Journal of astronautics. – 1990. No 3. P. 2-9.
4. Yan Mufu. Mathematical model of plasma nitriding and computer simulation. // Dissertation for master. – Harbin, 1987. – P. 124.
5. Dai Yanan. Mathematical model of plasma nitriding of low alloy steel and computer simulation. // Dissertation for master. – Harbin, 2002. – P. 190.
6. Бокштейн Б.С. Диффузия в металлах. – М.: Металлургия, 1978. – 248 с.