ПОВЫШЕНИЕ ЭФФЕКТИВНОСТИ ЛЕЗВИЙНОЙ ОБРАБОТКИ И СНИЖЕНИЕ ИЗНОСА ИНСТРУМЕНТА ЗА СЧЕТ АКТИВАЦИИ СОТС
Киселева Е.В. (ИГЭУ, г. Иваново, РФ)
The mehaniko-likelihood model allowing qualitatively to explain efficiency of small disperse emulsions in formation of a boundary lubricant layer, at a penetration stage is offered. The role of the superficial phenomena reveals at reduction of the size of particles of a technological liquid.
С целью повышения технологических возможностей смазочно-охлаждающих технологических средств (СОТС) и улучшения их реологических свойств было разработано устройство (рис.1), которое обеспечивает значительную турбулизацию потоков жидкости и дополнительные ускоренные потоки. Процессы перемешивания СОТС сопровождаются явлениями кавитации, которые возникают в результате местного понижения давления жидкости при увеличении скорости ее прохождения через специальные сопла (гидродинамическая кавитация).
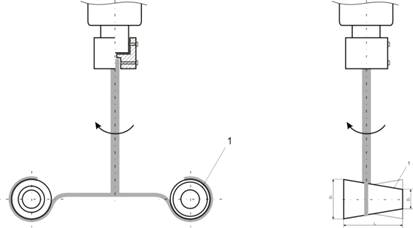
Рисунок 1 - Смеситель: 1-рабочий орган смесителя
Смеситель позволяет получать более дисперсные составы, тем самым, повышая их стабильность, уменьшая расслаивание эмульсий и суспензий и значительно повышает технологические параметры процесса резания.
Известно, что приготовление водоэмульсионных смазочно-охлаждающих технологических средств (СОТС) с использование интенсивного диспергирования существенно повышает триботехнические характеристики этого смазочного материала при операциях лезвийного резания [1]. Предполагается, что объяснения этих результатов могут лежать в области механохимии, однако детальный механизм этого явления до сих пор не вполне ясен. Анализ возможных моделей специфики смазочного действия микродисперсных эмульсий показывает, что возможно проявление следующих эффектов
1) Влияние размера частиц на механическую кинетику проникновения дисперсной фазы в контактную зону.
2) Воздействие избытка поверхностной энергии дисперсной системы на ее теплофизические характеристики.
3) Изменение химической кинетики процесса образования адсорбционного граничного смазочного слоя.
Не исключено, что все три перечисленных выше механизма действуют в реальном процессе резания. Рассмотрим в настоящей работе первый, наиболее простой механизм, который может быть объяснен в рамках микрокапиллярной модели контакта между стружкой и инструментом [2]. Проникающая способность является одной из основных характеристик СОТС. От того, насколько близко к зоне контакта проникнет смазка, зависит эффективность используемой смазочной композиции.
Каналом проникновения смазки на границу раздела "стружка-инструмент" является динамическая сеть межповерхностных капилляров. При этом капиллярный поток смазки, движущийся по границе раздела между передней поверхностью инструмента и стружкой от зоны отрыва стружки к режущей кромке, является наиболее трибологически значимым.
Единичный капилляр можно представить в виде цилиндра, один конец которого закрыт. Такой капилляр имеет характерные размеры r и l. Если длина капилляра l не является доминирующим фактором, то его радиус r может ограничивать размеры проникающих в капилляр дисперсных частиц, входящих в состав СОТС. Наличие крупных частиц снижает вероятность эффективного заполнения капиллярной сети трибоактивной фазой. Покажем, как принципиально отличается характер проникновения в капиллярную сеть эмульсионных СОТС при различных соотношениях размера частиц масляной фазы R и радиуса капилляра r.
Случай 1. Крупные частицы. R >> r.
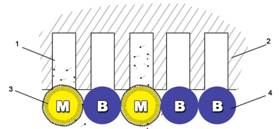
Пусть в какой-то момент времени контактная зона имеет NК капилляров, у каждого из которых открытый конец обращен в сторону смазочной среды. Поскольку частицы масляной фазы крупные, часть капилляров будут заполнены исключительно масляной фазой, а оставшаяся их часть —только лишь водой (рис. 2, а). Пропорция между этими частями будет соответствовать концентрации с масла в воде. Поскольку трибоактивный компонент будет действовать только в Nk ∙ c капилляров, коэффициент сопротивления сдвигу в такой капиллярной системе будет пропорционально числу капилляров заполненных маслом, и это будет отражено величиной кажущегося коэффициента трения стружки по передней поверхности.
Случай 2. Мелкие частицы. R << r.
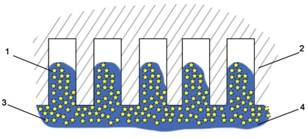
В данном случае в каждый капилляр обязательно попадут и масло, и водная фаза. Поскольку для адсорбции масляной фазы ее необходимо немного, чтобы покрыть всю поверхность, то граничный смазочный слой будет образован масляной фазой в каждом капилляре (рис. 2, б).
|
а |
|
б |
|
|
Рисунок 2- Механизм проникновения эмульсии: а – когда диаметр масляной фазы больше диаметра капилляра; б – когда диаметр масляной фазы меньше диаметра капилляра; 1 – единичный капилляр: 2 – сеть капилляров между поверхностью стружки и передней поверхностью инструмента; 3 – масляная фаза; 4 – водная фаза |
|||
Согласно нашей гипотезе, сопротивление сдвигу будет находиться в прямой зависимости от следующих факторов:
τ = f (NК; С; d; r) (1)
где φ – коэффициент сопротивления сдвигу; NК – количество открытых капилляров на межфазной границе в данный момент времени; с – концентрация масляной фазы; d – дисперсность частиц; r – радиус капилляра.
Рассмотрим энергетический аспект изучаемой нами проблемы. В гетерогенных системах (какими являются изучаемые эмульсии), одна из фаз представляет собой сравнительно крупные частицы, поверхность раздела фаз невелика. В таких системах поверхностные явления практически не проявляются. По мере уменьшения размеров частиц вещества одной из фаз возрастает абсолютная величина поверхности раздела и поверхностные свойства приобретают все большее значение. Поверхностные явления связаны с наличием избыточной энергии у поверхности раздела фаз.
Дисперсность D масляной фазы в СОТС линейно связана с удельной поверхностью Sуд для шарообразных частиц:
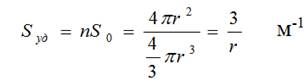 (2)
(2)
где n – число частиц, S0 – поверхность каждой частицы.
Фактором интенсивности при определении поверхностной энергии является поверхностное натяжение. Для гетерогенной системы полное изменение внутренней энергии (изобарно-изотермный потенциал Гиббса) будет записываться следующим образом [4]:
dU = TdS
– pdV + σds
+ ![]() + φdq,
(3)
+ φdq,
(3)
где dU − изменение внутренней энергии; Т − температура; dS – изменение энтропии; p − давление; dV − изменение объема; σ − поверхностное натяжение; ds − изменение площади поверхности; µi − химический потенциал компонента i; dni − изменение количества вещества компонентов; φ − электрический потенциал; dq − изменение заряда. При постоянных S, V, ni и q имеем
 (4)
(4)
т.е. поверхностное натяжение есть частная производная от внутренней энергии по площади поверхности раздела фаз при постоянных энтропии, объеме, количестве вещества и заряде.
Допустим, что размер частиц крупнодисперсной эмульсии составляет 100 мкм, а мелкодисперсной 1 мкм (что примерно соответствует нашим экспериментальным данным). Поверхностное натяжение на границе масло–вода составляет 0,0336 Дж/м2. Тогда будет происходить изменение поверхностной энергии, связанной с совершением работы против сил внутреннего давления (рис. 3).
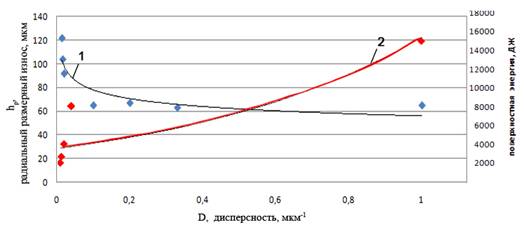
Рисунок 3- Корреляция между поверхностной энергии системы и износом инструмента: 1 – зависимость износа инструмента от дисперсности; 2 – зависимость поверхностной энергии от дисперсности эмульсии. Исследование: точение стали 12Х18Н10Т резцами ВК8. Режимы резания: скорость резания v = 270 м/мин; подача s = 0,1 мм/об.; глубина резания t = 0,5 мм
Эта запасенная энергия влияет на физико-химическую кинетику многоступенчатого смазочного процесса, описанного в микрокапиллярной модели смазочного действия СОТС.
При увеличении межфазной поверхности ускоряются различные физико-химические явления, в том числе облегчается испарение. При быстром испарении, больше времени будет оставаться на заполнение капилляра, образование адсорбционного граничного слоя.
Литература
3. Фридрихсберг, Д.А. Курс коллоидной химии / Д.А. Фридрихберг. – Л.: Химия, 1984. – с.146
4. Ребиндер, П.А. Физико-химическая механика дисперсных структур / П.А. Ребиндер. - М.: Наука, 1966. – с. 53-66.