РЕГРЕССИОННО-КОРРЕЛЯЦИОННАЯ МОДЕЛЬ ПАРАМЕТРОВ

УПРОЧНЕНИЯ СТАЛЬНЫХ ПОВЕРХНОСТЕЙ МЕТОДОМ

ЭЛЕКТРОИСКРОВОГО ЛЕГИРОВАНИЯ

 

Иванова Е.В., Коротаев Д.Н. (СибАДИ, г. Омск, РФ)

 

The plural regressionno-correlation analysis of parameters of an electrospark alloying is carried out. It is established that significant factors for hardening of steel surfaces are the working current and a thickness of the alloyed layer.

 

Долговечность деталей машин и инструментов в значительной степени зависит от износостойкости материалов, из которых они изготовлены. Перспективными методами поверхностного упрочнения стальных поверхностей являются методы, основанные на обработке материалов концентрированными потоками энергии и вещества. К числу таких методов относится электроискровое легирование (ЭИЛ), позволяющее получать поверхностные слои с уникальными физико-механическими и триботехническими свойствами [1].

Моделирование процессов упрочнения активно используется при исследовании, разработке и усовершенствовании упрочняющих технологий. Развитие методов моделирования многофакторных процессов в многокомпонентных гетерогенных системах дает возможность проводить «активный» эксперимент и значительно сокращает время исследований [2]. Наибольшее распространение в инженерии поверхности получили формальные модели, основанные на математической статистике (обработка экспериментальных результатов) и оптимизации (планирование экспериментов, корреляционный и регрессионный анализы).

Множественной корреляционной связью является связь между несколькими факторными (x₁, x₂, … x_k) и одним результативным признаком y. Такую связь характеризует матрица парных коэффициентов корреляции (табл. 1).

 

Таблица 1 – Матрица парных коэффициентов корреляции

Факторы	y	x1	x2	…	xk
y	1	r01	r02	…	r0k
x1	r10	1	r12	…	r1k
x2	r20	r21	1	…	r2k
…	…	…	…	…	…
xk	rk0	rk1	rk2	…	1

В таблице величины r_ij являются линейными коэффициентами корреляции и характеризуют силу линейной связи между i-м и j-м признаками. По главной диагонали таблицы всегда будут располагаться значения, равные единице, так как связь между одноименными признаками будет функциональной. Таблица является «симметричной» относительно главной диагонали, т.е. r₀₁ = r_10, r₂₁ = r₁₂ и т.д.

Анализ таблицы необходимо начинать с первой строки: в ней отражена сила влияния каждого из факторных признаков на результативный признак. Очевидно, что слабыми связями можно пренебречь и исключить соответствующие признаки-факторы из дальнейшего рассмотрения.

Необходимо также исключить мультиколлениарность (коррелированность факторных признаков между собой). В качестве критерия отсутствия мультиколлениарности используется соблюдение следующих неравенств:

 и .

Сравниваются абсолютные значения линейных коэффициентов корреляции. Если не выполняется одно из неравенств, то исключается тот факторный признак, который менее сильно коррелирует с результативным признаком.

В настоящей работе результативным признаком является скорость изнашивания J × 10^-3 мм/мин (y), исследуемыми факторами: рабочий ток I, А (x₁), толщина легированного слоя d, мкм (x₂), длительность искрового разряда t, мкс (x₃), микротвердость покрытия m, ГПа (x₄), сила адгезии F, нН (x₅).

Группировка экспериментальных и расчетных статистических данных представлена в табл. 2.

 

Таблица 2 – Аналитическая группировка данных, полученных при ЭИЛ стальных образцов

Факторы	y,×10-3 мм/мин	x1, А	x2, мкм	x3, мкс	x4, ГПа	x5, нН
1	6	0,3	35	118	15,7	90
2	5,2	0,35	41	123	11,5	130
3	4,7	0,4	47	105	11,5	150
4	4,3	0,5	53	123	15,7	122
5	4,2	0,55	55	105	17,3	85
6	4	0,66	62	118	17,3	76
Итого	28,4	2,7	293	692	89	653
Ср. знач.	4,73	0,5	48,8	115,3	14,8	108,8
Ср. кв. откл., S	0,69	0,1	9,0	7,6	2,4	26,8
Коэф. вариации	14,5	24,0	18,4	6,6	16,5	24,6

Так как коэффициент вариации не превышает 33 %, то совокупность является однородной и среднее значение факторов – надежно.

Результаты расчетов r представлены в корреляционной матрице (табл.3).

В результате проверки критерия отсутствия мультиколлениарности, оказалось, что реально на переменную y оказывают влияние факторы – х₁ (рабочий ток), х₂ (толщина легированного покрытия) и х₃ (длительность искрового разряда).

Каноническое уравнение множественной регрессии имеет следующий вид:

.

Раскрывая скобки и приводя подобные слагаемые, получим обычный вид множественного уравнения регрессии:

.

Коэффициенты уравнения множественной регрессии показывают абсолютную величину влияния факторов на уровень результативного признака, и характеризуют степень влияния каждого фактора на анализируемый показатель при фиксированном среднем уровне других факторов.

Получены множественный коэффициент корреляции R_m и множественные коэффициенты регрессии (b₁ – b₅).

R_m = 0,98; b₁ = - 9,941; b₂ = 0,030; b₃ = 0,001; b₄ = 0,040; b₅ = - 0,008.

 

Таблица 3 – Корреляционная матрица

Факторы	y	x1	x2	х3	х4	x5
y	1	-0,94	-0,97	0,24	-0,38	0,14
x1	0,94	1	-0,99	0,18	-0,65	0,46
x2	0,97	0,99	1	0,18	-0,54	0,35
х3	-0,24	-0,18	-0,18	1	0,01	0,04
x4	0,38	0,65	0,54	-0,01	1	0,90
x5	-0,14	-0,46	-0,35	-0,04	-0,90	1

Для сравнения роли различных факторов в формировании изучаемого показателя необходимо дополнить абсолютные величины относительными. Например, частные коэффициенты эластичности показывают, насколько процентов, в среднем, изменяется показатель y с изменением признака x_i на один процент при фиксированном положении других факторов, и рассчитывается по формуле:

,

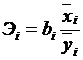где b_i – коэффициент регрессии при i-м факторе.

b-коэффициенты показывают, на какую часть среднеквадратического отклонения изменится переменная y с изменением соответствующего фактора x на величину среднеквадратического отклонения. Этот коэффициент позволяет сравнивать влияние колебания различных факторов на вариацию исследуемого показателя, что позволяет выявить факторы, в развитии которых заложены наибольшие резервы изменения результативного показателя:

,

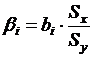где S_x и S_y – среднеквадратические отклонения.

Чтобы оценить долю влияния каждого фактора в суммарном влиянии факторов, включенных в уравнение регрессии, рассчитываются D-коэффициенты:

,

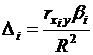где  - коэффициент корреляции; R² – коэффициент детерминации.

Результаты расчета и ранжирование относительных коэффициентов представлены в табл. 4.

Как видно из представленных результатов наибольшее влияние на скорость изнашивания обработанных ЭИЛ поверхностей оказывают: х₁ (рабочий ток), х₂ (толщина легированного покрытия).

 

 Таблица 4 – Относительные коэффициенты и ранг факторов

Факторы	Значения коэффициентов			Ранг факторов по величине коэффициентов			Средний ранг
	Эi	bi	Di	Эi	bi	Di
x1	1,06	1,42	1,36	1	1	1	1
x2	0,31	0,39	0,39	2	2	2	2
x3	0,02	0,01	0,002	5	5	5	5
x4	0,13	0,14	0,05	4	4	3	4
x5	0,19	0,31	0,04	3	3	4	3

Следовательно, уравнение в каноническом виде с учетом наиболее значимых факторов будет выглядеть следующим образом:

y- 4,73 = -9,941(x₁ – 0,5) + 0,030(x₂ – 48,8).

В натуральном виде:

y = -9,941x₁  + 0,030x₂ + 8,24.

Таким образом, при увеличении рабочего тока на 0,1 А скорость изнашивания поверхности уменьшится в среднем на 9,941·10^-3 мм/мин; при увеличении толщины легированного слоя на 1 мкм скорость изнашивания повысится на 0,030·10^-3 мм/мин.

Литература

1.Верхотуров А.Д. Технология электроискрового легирования металлических поверхностей / А.Д. Верхотуров, И.М. Муха. – Киев: Техника, 1988. – 181 с.

2. Хина Б.Б. Математическое моделирование синтеза покрытий и материалов: от твердофазной диффузии к механизмам фазообразования (по материалам работ проф. Л.Г. Ворошнина) / Б.Б. Хина, Б.М. Хусид // Упрочняющие технологии и покрытия. – 2008. - № 1. – С. 8–14.