ПРИМЕНЕНИЕ ПОЛЯРИЗАЦИОННЫХ МЕТОДОВ АНАЛИЗА КОЛЕБАТЕЛЬНЫХ ТРАЕКТОРИЙ ДЕТАЛЕЙ МАШИН

 

Фирсов Г.И. (ИМАШ РАН, г.Москва, РФ)

 

The use of polarization methods for the study of the trajectories of the moving machine parts is examined. For the total determination of elliptical polarization is calculated the orientation of ellipsis in its own plane, form, direction of circuit and size of ellipsis. Results can be used for diagnostics of state and assembling of machines.

 

Каждая движущаяся точка колеблющегося тела последовательно занимает различные положения в пространстве. Совокупность этих положений за конечный отрезок времени определяет некоторую линию или фигуру - траекторию, которая содержит ценную информацию о характере движения, об особенностях колебательной системы и внешних воздействиях [1]. Анализ траектории облегчает выбор адекватного математического описания колебательной системы в задачах моделирования колебаний, а при решении ряда практических задач позволяет разработать рекомендации по совершенствованию конструкции с целью обеспечения требуемого режима работы. Пусть некоторая точка участвует одновременно в двух колебательных движениях колебаний x(t) и y(t), определяющих соответственно декартовые координаты точки на плоскости. Тогда движущаяся точка будет вычерчивать некоторую фигуру или совокупность фигур Лиссажу, каждая из проекций которых на взаимно перпендикулярные координатные оси является одномерным колебательным процессом. Получаемая траектория характеризует геометрию колебательного движения на плоскости и широко применяется для исследования особенностей изменяющихся положений центра тяжести (точки) колебательной системы, изменяющихся положений конца суммарного вектора по его двум проекциям, кинематического движения валов и других вращающихся элементов в их поперечной плоскости, колебаний трубок в пучке, виброперемещений тела при его вибротранспортировании и т.д. Наряду с указанными видами геометрических траекторий реальных или воображаемых точек, при исследовании динамических систем большое значение имеют траектории на фазовой плоскости, определяющие движение в обобщенных фазовых координатах, например, движение странного аттрактора.

Вследствие действия различных источников вибрации и неоднородности конструкции машины энергия взаимодействия между двумя наблюдаемыми процессами колебаний может существенно отличаться в разные моменты времени и на разных частотах. В общем случае плоское движение точки в различных направлениях оказывается различным, и исследуемая траектория может быть разложена на две субтраектории - полностью поляризованную (ППТ) и полностью неполяризованную (НПТ). ППТ отображается характерной ориентированной линией, фигурой или регулярно повторяющимися фигурами вследствие, например, корреляции суммируемых колебательных процессов. Наличие даже слабой корреляции из-за связанности колебаний порождает определенные закономерности в изображении частично поляризованной траектории в виде некоторой фигуры, например, эллиптического или кругового кольца, или размытой прямой линии. НПТ определяется несвязанными колебаниями равного уровня и поэтому вместо характерной формы дает случайное сплошное круговое заполнение участка плоскости, в большинстве случаев в соответствии с нормальным двумерным законом распределения [2].

Для количественной оценки параметров поляризованной части траектории удобно перейти от вещественных колебательных процессов к соответствующим комплексным (векторным) представлениям, например, в виде аналитических сигналов: X(t) = x(t) + jx_г(t), Y(t) = y(t) + jy_г(t), где x_г(t), y_г(t) - процессы, преобразованные по Гильберту [3]. При этом частично поляризованная траектория связана с корреляционной матрицей, состоящей из математических ожиданий попарных произведений аналитических сигналов

 

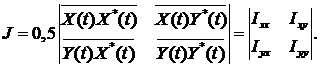
Здесь знаком * обозначены комплексно сопряженные аналитические сигналы. Диагональные элементы I_xx и I_yy матрицы действительны и представляют собой дисперсии процессов соответственно в направлении x и y, поэтому след матрицы J определяет след траектории на плоскости:  Недиагональные комплексно сопряженные элементы I_xy и I_yx определяются взаимной корреляцией между x- и y-компонентами; детерминант матрицы J имеет положительную действительную величину:  где r_xy - коэффициент корреляции между колебательными процессами x(t) и y(t). След поляризованной части траектории определяется выражением I_п = (sp²J - 4detJ)^1/2, 0 £ I_п £ spJ, откуда получаем величину степени поляризации траектории

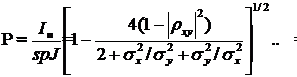
Для ППТ P = 1, для НПТ P = 0. Большие значения степени поляризации соответствуют большему стягиванию кольцевидной траектории в одну линию, имеющую форму, например, эллипса, круга или прямой. Рассмотренный выше метод исследования траекторий выявляет некоторые общие (интегральные) свойства поляризации, характерные для всего осредняемого движения в целом в течение достаточно большого отрезка времени. Вместе с тем свойства траектории могут существенно изменяться во времени. На координатной плоскости будут наблюдаться различные сменяемые друг друга фигуры. Для более детального исследования инерционной связи двух колебательных процессов и описания траектории точки, участвующей одновременно в двух ортогональных частично когерентных движениях, заданных в форме аналитического сигнала: X(t) и Y(t), введем понятие поляризационной переменной c(t): c(t) = Y(t) / X(t) = |c(t)| , где |c(t)| = A_y(t) / A_x(t) - модуль, равный отношению мгновенных амплитуд, q(t) - разность мгновенных фаз колебаний y(t) и x(t). Когда плоское движение представлено двумя когерентными колебаниями вдоль двух ортогональных направлений то, в общем случае полностью поляризованная траектория в каждый момент времени имеет форму эллипса. Для полного определения эллиптической поляризации необходимо знать ориентацию эллипса в его собственной плоскости, форму, направление обхода и размер эллипса. Параметры эллипса в каждый момент времени определяются модулем и разностью фаз поляризационной переменной. Используя правило преобразования вектора при повороте системы координат, можно записать выражение для поляризационной переменной в виде комплексной функции двух действительных аргументов: азимута q_A и эллиптичности E: c = (tgq_A + jE) / (1 - jE tgq_A). Следовательно, каждому комплексному числу для каждого момента времени можно поставить в соответствие эллиптическое состояние поляризации с заданными параметрами. Чтобы определить азимут q_A и эллиптичность E эллипса поляризации, представленного данной точкой на комплексной плоскости, необходимо обратить последнее выражение. Тогда азимут эллипса q_A, как угол между большой его осью и положительным направлением оси x, определится по формуле q_A = 0,5 arctg [2 Re(c) / (1 - |c |²]. Отношение длин малой b и большой a полуосей эллипса дает величину эллиптичности траектории E = b/a, (0 £ |E| £ 1). Удобно ввести угол эллиптичности, определяемый равенством e_E = 0,5 arcsin [2 Im(c) / (1 + |c|²)]. Таким образом, использование понятия поляризационной переменной траектории позволяет определить азимут, эллиптичность, направление обхода, размеры осей и площадь эллипса поляризации как функции времени.

На практике обозначение направления обхода траектории часто совмещают с выражением эллиптичности, условно полагая, что положительная эллиптичность соответствует правой (по часовой стрелке) поляризации и наоборот. Правая поляризация будет соответствовать положительному значению фазового угла поляризационной переменной, когда колебание вдоль оси x отстает по фазе от колебания вдоль оси y. Размер эллипса поляризации определяется величинами малой и большой его полуосей

 

где A_x, A_y - мгновенные амплитуды колебаний соответственно в направлении x, y. Величина площади эллипса поляризации определяется по формуле S_E = pab.

Для определения динамической поляризации в виде АФЧХ целесообразно воспользоваться методами спектрального анализа. В результате получаем возможность оценить действительную и мнимую части динамической поляризации с последующим определением спектров параметров эллипса поляризации. Аналогом степени поляризации траектории является величина функции когерентности  рассматриваемых колебательных процессов, которая на каждой частоте характеризует степень линейной связи двух процессов. Сумма квадратов средних значений амплитуд a и b когерентных случайных колебаний может быть записана в виде  где  - соответственно дисперсия полностью когерентных компонент колебаний x(t) и y(t) в некотором частотном диапазоне. С учетом равенства Парсеваля и неравенства Коши получаем следующую оценку снизу для размера эллипса поляризации в заданном частотном диапазоне от f_min до f_max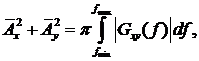  

где  - модуль взаимной спектральной плотности, а  - спектральные плотности колебаний x(t) и y(t). Таким образом, можно рассматривать q_A, E, направление обхода, a, b и S_E как функции частоты и решить задачу о влиянии частотного состава компонент движения на результирующую траекторию.

На основе предлагаемой методики определения параметров траекторий было проведено моделирование в среде MATLAB. В качестве тестового примера использовался двумерный процесс x(t) = A_xsinwt, y(t) = A_ysin(wt + j), длина реализации составила 1024, значения отношения амплитуд колебаний и фазы принимали варьировались в пределах 0,5 - 1 и 20° - 120° соответственно. Сравнение полученных значений азимута, эллиптичности, длины большой полуоси и площади эллипса поляризации с расчетными показали хорошее совпадение. Различие значений длины большой полуоси и площади эллипса объясняются тем, что расчетные формулы соответствуют нормальному случайному процессу, а модельный эксперимент выполнялся с гармоническими функциями. Пересчет значений дисперсии и математического ожидания показал хорошее совпадение результатов. Изложенный метод использовался для анализа динамической погрешности позиционирования промышленного робота типа «Пума-560», позволившего выявить частоты колебаний, на которых эллипсы поляризации имеют максимальную площадь. При этом большая ось эллипсов поляризации располагается перпендикулярно линии движения схвата робота при подходе к номинальной точке.

Литература

1. Микишев Г.Н. Экспериментальные методы в динамике космических аппаратов. - М.: Машиностроение, 1978. - 248 с.

2. Добрынин С.А., Фельдман М.С., Фирсов Г.И. Методы автоматизированного анализа вибрации машин. - М.: Машиностроение, 1987. – 221 с.

3. Panter P. Modulation, Noise, and Spectral Analysis. Applied to Information Transmission. - New York: McGraw-Hill, 1965. - 760 p.