МОДЕЛИРОВАНИЕ УСТОЙЧИВОСТИ ВАЛОЧНО- ПАКЕТИРУЮЩЕЙ МАШИНЫ, ОСУЩЕСТВЛЯЮЩЕЙ ВЫВОЗ ДЕРЕВА В ВЕРТИКАЛЬНОМ ПОЛОЖЕНИИ

 

Онучин Е. М., Ласточкин Д. М., Перетягин П. А., Зайнуллин А.Д. (МарГТУ, Йошкар-Ола, РФ)

 

This article describes the mathematical modeling methods used in the design of the machine "Ru.Les" for its sustainability in the removal of the tree in an upright position.

 

Перспективным способом обеспечения устойчивости машины, вывозящей дерево в вертикальном положении, является компенсация случайных воздействий, создающих опрокидывающий момент при помощи специальной автоматической системы. Устойчивость системы «Робот «Ru.Лес» – Дерево» достигается за счет системы автоматического управления захватно-срезающим устройством, которая обеспечивает не передачу колебаний корпуса машины в вертикальных продольной и поперечной плоскостях, вызванных неровностями микрорельефа опорных поверхности под колесами машины, на дерево. Принцип работы системы автоматического управления заключается в приведении захватно-срезающего устройства с деревом в строго вертикальное положение вне зависимости от наклонов и колебаний корпуса машины, что позволяет сохранять устойчивость лесного робота с деревом при его транспортировании.

Эффективность использования системы автоматического управления захватно-срезающим устройством можно определить путём сравнения значений предельно допустимых (при которых ещё сохраняется устойчивое состояние системы) наклонов и колебаний корпуса машины для машин без системы выравнивания дерева и с системой выравнивания дерева в вертикальном положении.

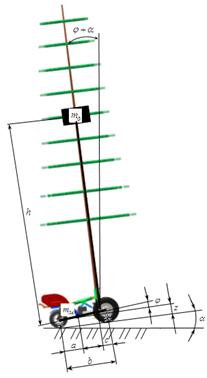
Статическая расчетная схема на устойчивость системы «Машина –Дерево» без системы автоматического управления захватно-срезающим устройством показана на рисунке 1.

Уравнение равновесия для данной системы будет иметь следующий вид:

,          (1)

где  – реакция на дальнем колесе самоходного шасси,  – масса машины,  – масса дерева, a, b, h, z – расстояния, g – ускорение силы тяжести.

Предельный угол , при котором машина находится в неустойчивом состоянии находится из данного выражения при :

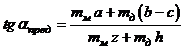.                                                          (2)

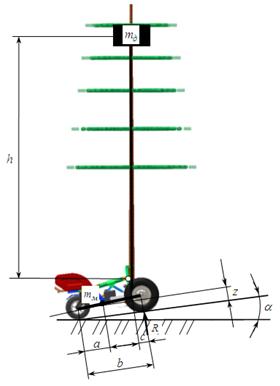
Статическая расчетная схема на устойчивость системы «Машина –Дерево» с системой автоматического управления захватно-срезающим устройством показана на рисунке 2.

Рисунок 1 – Расчётная схема статической устойчивости робота «Ru.Лес» с транспортируемым деревом (без системы автоматического управления захватно-срезающим устройством)	Рисунок 2 – Расчётная схема статической устойчивости робота «Ru.Лес» с транспортируемым деревом (с системой автоматического управления захватно-срезающим устройством)

 

Уравнение равновесия для данной системы будет иметь следующий вид:

                          (3)

Предельный угол  в данном случае будет находиться по следующей формуле:

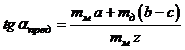.                                                          (4)

Статический расчет устойчивости лесных машин, транспортирующих деревья в вертикальном положении, показывает, что использование системы автоматического управления, поддерживающей дерево в положении, близком к вертикальному, значительно увеличивает размеры деревьев, с которыми машина сохраняет устойчивость.

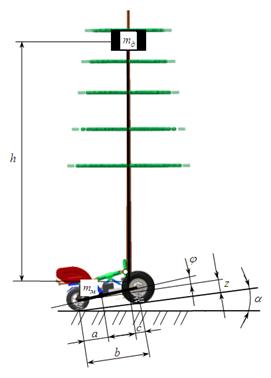
Для исследования динамической устойчивости системы «Машина – Дерево» были рассмотрены две плоские схемы (рисунке 3 и 4). В обеих схемах рассматриваемая система имеет две степени свободы – возможность вертикальных и угловых колебаний в плоскости чертежа.

Представление в рассматриваемых схемах дерева как абсолютно жесткого стержня оправдано, так как при определённой линеаризации системы (считаем угловые колебания малыми) учёт дополнительной степени свободы, связанной с упругостью перемещаемого дерева, не оказывает влияния на первые две обобщенные координаты в силу распада системы уравнений на независимые группы.

Рисунок 3 – Расчётная схема динамической устойчивости робота «Ru.Лес» с транспортируемым деревом (без системы автоматического управления захватно-срезающим устройством)	Рисунок 4 – Расчётная схема динамической устойчивости робота «Ru.Лес» с транспортируемым деревом (с системой автоматического управления захватно-срезающим устройством)

Для моделирования динамической устойчивости рассматриваемой системы целесообразно использование метода уравнений Лагранжа второго рода. Кинетическая энергия плоской системы, представленной на рисунке 3, равна:

,        (5)

а потенциальная энергия:

                                                    (6)

где  – момент инерции машины относительно поперечной горизонтальной оси, проходящей через центр тяжести машины;  – приведённая длина упругих элементов подвески в ненагруженном состоянии; ,  – приведённая жёсткость упругих элементов подвески.

Частные производные от кинетической и потенциальной энергий:

,                                    (7)

,

,                         (8)

Система уравнений Лагранжа второго рода для рассматриваемой схемы:

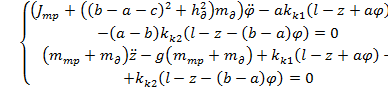,                (9)

Расчётная схема, представленная на рисунке 4, отличается от рассмотренной тем, что угловые колебания машины не передаются на дерево (считаем работу системы автоматического управления захватно-срезающим устройством идеальной).

Кинетическая и потенциальная энергия системы в данном случае

,                                                   (10)

а потенциальная энергия

,                                                                 (11)

где  – момент инерции машины относительно поперечной горизонтальной оси, проходящей через центр тяжести машины;  – приведённая длина упругих элементов подвески в ненагруженном состоянии; ,  – приведённая жёсткость упругих элементов подвески.

Частные производные от кинетической и потенциальной энергий:

,

,                                                              (12)

,

.

Система уравнений Лагранжа второго рода для рассматриваемой схемы:

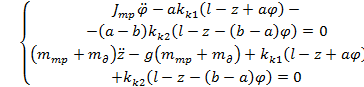,                     (13)

С точки зрения динамики системы «Машина – Дерево», идеальная работа системы автоматического управления захватно-срезающим устройством приводит к тому, что резко на величину  уменьшается момент инерции системы относительной поперечной горизонтальной оси, проходящей через центр тяжести машины. При этом становится возможным рассмотрение массы дерева не как поднятой на высоту h относительно высоты центра тяжести машины, а приложенной на том же уровне z, что позволяет сделать вывод о качественном увеличении динамической устойчивости системы.

Работа выполнена при финансовой поддержке министерства образования и науки РФ в рамках НИР по государственному контракту №16.515.11.5053