АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ ОПТИМИЗАЦИИ РАСКРОЯ ПИЛОВОЧНИКА С ВЫПИЛИВАНИЕМ ТРЕХ БРУСЬЕВ И ТРЕХ ПАР БОКОВЫХ ДОСОК

 

Агапов А.И. (ВятГУ, г.Киров, РФ)

 

Developed an algorithm for solving the optimization problem with cutting sawlogs Cutting three bars and three pairs of lateral plates.

 

При раскрое пиловочника больших размеров (60…100см) брусово-развальным способом целесообразно выпиливать три одинаковых по толщине бруса, а из боковой части бревна можно получить еще три пары досок. Важно знать оптимальные размеры брусьев и досок. Для решения поставленной задачи составляем математическую модель. В качестве критерия оптимальности выбираем объемный выход четырехкантных брусьев и боковых обрезных досок, получаемых при первом проходе брусово-развального способа раскроя бревна. Целевую функцию можно записать в виде суммы площадей поперечных сечений трех брусьев и трех пар боковых обрезных досок

                                                      (1)

где      Н – толщина бруса, А₁ – ширина пласти центрального бруса, А₂ –  ширина наружной пласти боковых брусьев, Т₁, Т₂, Т₃ – толщина соответственно первой, второй и третьей пары боковых досок, b₁, b₂, b₃ – ширина наружных пластей соответственно первой, второй и третьей пары боковых досок.

Для составления уравнений связи воспользуемся теоремой Пифагора. Взаимосвязь диаметра бревна в вершинном торце с размерами брусьев и досок можно представить следующими уравнениями

                                                                                                (2)

                                                                                              (3)

                                                                          (4)

                                         (5)

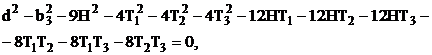                                   (6)

где d – диаметр бревна в вершинном торце.

         Полагаем, что математическая модель составлена.

         Для решения данной модели воспользуемся методом множителей Лагранжа. Функцию Лагранжа представляем в следующем виде

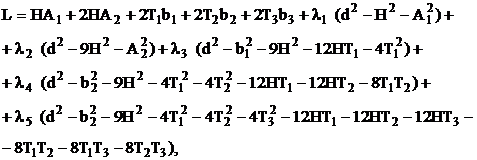                          (7)

где λ₁ λ₂ λ₃ λ₄ –множители Лагранжа.

Находим частные производные и приравниваем их к нулю

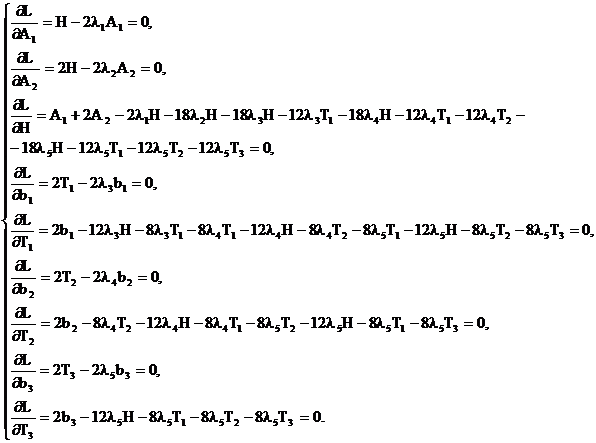(8)

Решаем систему уравнений (8) совместно с уравнениями связи. Рассматриваем предпоследнее уравнение системы (8)

                            ,                                                        (9)

Рассматриваем последнее уравнение системы (8), в которое подставляем выражение (9)

                        (10)

Рассматриваем шестое уравнение системы (8)

                            ,                      .                                 (11)

Рассматриваем седьмое уравнение системы (8), которое с учетом выражения (11) можно представить в следующем виде

                                                               (12)

Зная ширину второй доски можно определить ширину третьей доски по формуле

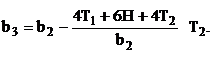                                                                      (13)

Рассматриваем четвертое уравнение системы (8)

                            ,                                                         (14)

Рассматриваем пятое уравнение системы (8), из которого определяем ширину второй доски

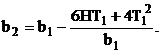                                                                                 (15)

Зная ширину второй пары досок b₂, используем уравнение связи (5) и определяем толщину этих досок

                                                                     (16)

Рассматриваем первое уравнение системы (8)

                                      ,                                            (17)

Рассматриваем второе уравнение системы (8)

                            ,                                                       (18)

Рассматриваем третье уравнение системы (8), которое с учетом множителей Лагранжа и  представляем в следующем виде

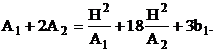                                                                      (19)

Из последнего равенства можно определить ширину первой доски

                                                             (20)

Из уравнения связи (2) можно написать

                                                                                          (21)

Из уравнения связи (3) можно написать

                                                                                          (22)

Определив ширину пластей брусьев А₁ и А₂, можно определить по формуле (20) ширину первой доски. Пользуясь уравнением связи (4) можно определить толщину первой доски по формуле

                                                                                (23)

По формуле (13) можно определить ширину третьей доски b₃, а затем воспользуемся уравнением связи (6) определяем толщину третьей доски

                                                            (24)

Таким образом, рассмотрены все уравнения системы (8), а также уравнения связи и получены формулы для определения размеров брусьев и досок. Однако в этих формулах размеры брусьев и досок взаимосвязаны, что затрудняет нахождение оптимальных размеров. Для решения поставленной задачи воспользуемся численным методом. Для этого изменяем толщину бруса, а остальные размеры брусьев и досок, а также целевую функцию будем определять по полученным выше формулам. По результатам расчетов можно найти вариант, при котором получается максимальное значение целевой функции. Это и будет соответствовать оптимальным размерам брусьев и досок. Для облегчения расчетов и анализа результатов, полученные ранее формулы, представляем в относительных единицах, полагая отношение H/d=m_н.

Тогда алгоритм решения задачи будет иметь следующий вид.

Относительная ширина пласти центрального бруса

                                                                                   (25)

Относительная ширина наружной пласти бокового бруса

                                                                        (26)

Относительная ширина первой пары боковых досок

                                (27)

Относительная толщина первой пары досок

                                                           (28)

Относительная ширина второй пары досок

                                                   (29)

Относительная толщина второй пары досок

                                             (30)

Относительная ширина третьей пары досок

                                       (31)

Относительная толщина третьей пары досок

                                  (32)

Относительная площадь поперечных сечений брусьев

                                         (33)

Относительная площадь поперечных сечений досок

                                                     (34)

Суммарная относительная площадь поперечных сечений брусьев и досок

                                                                                     (35)

Таким образом, впервые разработан алгоритм для определения оптимальных размеров пилопродукции при раскрое пиловочника с выпиливанием трех брусьев и трех пар боковых досок.