МЕТОДИКА ИЗУЧЕНИЯ СТУДЕНТАМИ СТРОИТЕЛЬНЫХ СПЕЦИАЛЬНОСТЕЙ МАТРИЧНЫХ АЛГОРИТМОВ В ЭЛЕКТИВНОМ КУРСЕ «ДИНАМИКА И УСТОЙЧИВОСТЬ СООРУЖЕНИЙ»

 

Сенющенков М.А., Швачко С.Н. (БГИТА, г.Брянск, РФ)

 

Описана структура спецкурса  строительной механики “Динамика и устойчивость сооружений” и методика практического применения на лабораторных занятиях обширного программного обеспечения, наиболее подходящая для изучения матричных алгоритмов.

 

С 2008 года в БГИТА введены для студентов строительных специальностей ПГС и ГСХ на 4-м курсе 2 элективных семестровых спецкурса с закреплением материала каждого семестра двумя РПР и зачетом:

1)       “Динамика и устойчивость сооружений” в объеме 54 часов аудиторных занятий (лекций, практических и лабораторных) [4];

2)      “Численные методы решения задач строительной механики” в объеме 48 часов аудиторных занятий (лекций, практических и лабораторных).

К отдельным темам спецкурсов   удобно обращаться при изучении специальных дисциплин на старших курсах (САПР несущих конструкций, металлические конструкции, искусственные дорожные сооружения и другие).

В спецкурсе  “Динамика и устойчивость сооружений” нами сделан акцент на теоретическое изучение и понимание таких сложных явлений механики, как устойчивость и динамика, а также на практическое освоение матричных алгоритмов получения результатов расчета из исходных данных сооружений. Методические материалы [4-9] включают примеры выполнения двух РПР,  контрольные вопросы к изучаемым темам, справочные таблицы специальных функций для расчета рам на устойчивость, а также таблицы систематизации курсов устойчивости и линейной динамики [4].

Цель РПР №1 "Расчет плоской статически неопределимой рамы с центрально сжатыми стойками на устойчивость методом перемещений" [5,6] - освоение и закрепление методов расчета  стержневой системы на устойчивость.

Методический прием освоения студентами курса устойчивости сооружений  при вы­полнении РПР состоит в том, что операции подготовки исходных данных и выполнения основных расчетов на устойчивость статически неопределимой рамы выполняются вручную. Применение на лабораторных занятиях пакета MathCAD позволяет автоматизировать вычисление специальных функций [4, 5], определителя устойчивости 2-го порядка в графической форме и уточнение корней критического параметра устойчивости [6]. 

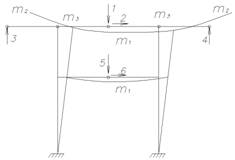
Важное значение при усвоении материала имеет   графи­ческое представление  двух форм потери устойчивости  плоской рамы. Важно также знать конечную цель расчета – это проверка устойчивости стоек рамы по СНиП [10] по значению сжимающей силы и величине расчетной (приведенной) длины стойки.

На лабораторных занятиях предусмотрено также применение лицензионного отраслевого пакета конечно-элементного анализа Stark_ES для автоматизированного расчета рамы на устойчивость по деформированной схеме и сравнение результатов с ручным расчетом для контроля.

Цель РПР №2 "Динамический расчет мно­гомассовой стержневой системы на собственные и вынужденные колебания" [7-9] - освоение и закрепление методов и алгоритмов расчета сооружений на собственные и вынужденные коле­бания на примере плоской рамы.

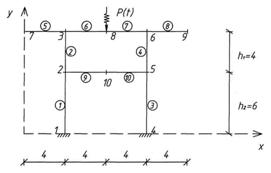
Методический прием освоения студентами курса динамики при вы­полнении РПР состоит в том, что все операции подготовки исходных данных и выполнения расчетов расчленены на промежуточные этапы с контролем результатов преподавателем.  Максимальное число динамических степе­ней свободы не превышает семи, что позволяет часть расчетов выполнить вручную (формирование матрицы податливости, вектора внешних нагрузок и матрицы масс).

Применение ЭВМ ограничено сложными разделами: расчетами статически неопределимой рамы, обращением матрицы подат­ливости, вычислением собственных значений и собственных векторов, расчетом на вынужденные колебания.  Важное значение при усвоении материала имеет   графи­ческое представление   спектров   частот   и   периодов колебаний, а главное - графи­ческое представление и анализ форм собственных колебаний плоской рамы.

Приведено два контрольных примера выполнения РПР: 1-й пример представлен в форме тестовой задачи с тремя степенями свободы и ручными аналитическими расчетами; 2-й пример представлен в форме прикладной задачи с 6-ю степенями свободы и автоматизированными статическими и динамическими расчетами.

 На лабораторных занятиях предусмотрено два сценария выполнения РПР с различным набором программного обеспечения, представленных ниже в таблице.

Промышленные пакеты программ ав­томатизированного выполнения расчетов сооружений на устойчивость и колебания (SCAD, STARK, NASTRAN и др.) рекомендуем применять студентам для сравнительного контроля РПР на лабораторных занятиях и при решении более простых тестовых задач. Практическое освоение расчетов сооружений по нормам [11, 12] более целесообразно проводить в  курсах САПР и на дипломном проектировании.

  

Алгоритмы расчета			Програм. обеспечение
№	Наименование этапа	Матричная запись	Сценарий 1	Сценарий 2
1	Подготовка исходных данных и выполнение статических расчетов
1.1	Установить число динамических степеней свободы "n" и сформировать динамическую модель рамы (аналитически и графически)
1.2	Сформировать вектор динамических нагрузок		Вручную
1.3	Сформировать вектор масс		Вручную
1.4	Сформировать дискретную систему для плоской рамы с номерами узлов, стержней, динамической нагрузкой, закреплениями, осями координат и размерами (аналитически и графически)
1.5	Сформировать таблицы исходных данных по узлам, стержням, сечениям и узловым силам		Вручную
1.5	Выполнить "n" расчетов рамы на воздействие единич­ных сил .		Intab13 [2]	STARK_ES [9]
1.6	Распечатать результаты (таблицы перемещений и усилий)		Intab13	STARK_ES
1.7	Распечатать в масштабе деформированные схемы рамы		Intab13	STARK_ES
1.8	Распечатать в масштабе единичные эпюры моментов		Intab13	STARK_ES
1.9	Нанести числовые значения на деформированные схемы		Вручную	Вручную
1.10	Нанести числовые значения на единичные эпюры моментов		Вручную	STARK_ES
1.11	Сформировать матрицу податливости А и проверить ее симметрию	А=	Вручную	Вручную
2	Определение частот и формы собственных колебаний
2.1	Ввести число динамических степеней свободы "n", вектор масс М, матрицу внешней податливости А.		SERVIK [8]	MathCAD [9]
2.2	Получить матрицу внешней жесткости рамы R обращением матрицы податливости А.	R = А-1	SERVIK	MathCAD
2.3	Получить несим­метричную матрицу динамической податливости С	С=А·М	SERVIK	MathCAD
2.4	Решить несимметричную проблему собствен­ных значений.		-	MathCAD
2.5	Произвести симметризацию матрицы динамической податливости C*	C*=М1/2·А· М1/2	SERVIK	-
2.6	Решить на ЭВМ симметричную проблему собственных значений,		SERVIK	-
2.7	Вывести на печать собственные значения λk и вектора		SERVIK	MathCAD
2.8	Изобразить спектральные шкалы частот собственных колебаний ωk, fk, периодов Тк.
2.9	Перейти к исходному базису собственных векторов		SERVIK	-
2.10	Произ­вести нормировку собственных векторов .		SERVIK	MathCAD
2.11	Сформировать вектора инерционных сил	,	вручную	MathCAD
2.12	Распечатать деформированные схемы рамы от статических сил инерции – формы колебаний		Intab13	STARK_ES
2.13	Распечатать таблицу перемещений		Intab13	STARK_ES
2.14	Нанести числовые значения на деф. схемы – формы колебаний		Вручную	Вручную
2.15	Проверить ортогональность двух любых форм колебаний ,		Вручную	Вручную
3	Расчет на вынужденные колебания методом разложе­ния по формам колебаний
3.1	Найти обобщенные массы Мk, для каждой формы колебаний		SERVIK	MathCAD
3.2	Найти обобщенные силы Qk(t) для каждой формы колебаний		SERVIK	MathCAD
3.3	Записать уравнения движения для каждой частоты собственных колебаний ωk в обобщенных координатах qк без демпфирования		SERVIK	MathCAD
3.4	Выбрать активную степень свободы, по которой задана динамическая нагрузка Р1 на динамической модели рамы		Вручную	Вручную
3.5а	Решить численно с помощью интеграла Дюамеля уравнения движения и найти обобщенные координаты qk(t) для P(t) = Ро = const	P(t) = Ро = const	SERVIK	-
3.5б	Решить численно с помощью аналитических формул уравнения движения и найти обобщенные координаты qk(t) для P(t) = Ро = const	P(t) = Ро = const	-	MathCAD
3.6	Получить численно компоненты вектора динамических перемещений  для всех учитываемых форм колебаний  через обобщенные координаты qk(t)		SERVIK	MathCAD
3.7	Изобразить осцилло­граммы zi(t) для компонент вектора динамических перемещений		SERVIK	MathCAD
3.8	Получить численно вектор упругих сил (t) через матрицу внешней жесткости R и вектор		SERVIK	MathCAD
3.9	Изобразить осцилло­грамму si(t) для активной компоненты вектора (t), соответствующей номеру загруженной степени свободы.		SERVIK	MathCAD
3.10	Установление параметров пика – максимального значения активной компоненты вектора упругих сил (si)max  и момента времени tпик.		SERVIK	MathCAD
3.11	Загрузить раму по направлению всех динамических степеней свобо­ды элементами вектора упругих сил max(tпик) и построить эпюру изгибающих моментов (Мдин)max в раме для момента времени tпик		Intab13	STARK_ES
3.12	Загрузить раму статической силой Ро и построить эпюру ста­тических изгибающих моментов Мст.		Intab13	STARK_ES
3.13	Найти динамический коэф­фициент μ в опасных сечениях рамы	μ=Мдин/Мст < 2	Вручную	Вручную
4	Сравнительный контроль частот и форм собственных колебаний прямым динамическим расчетом рамы по МКЭ
4.1	Сформировать дискретную систему для плоской рамы с номерами узлов, стержней, динамической нагрузкой, закреплениями, осями координат и размерами.		STARK_ES
4.2	Сформировать динамическую модель рамы с точечными массами		STARK_ES
4.3	Выполнить расчет плоской рамы на собственные колебания по МКЭ		STARK_ES
4.4	Распечатать спектры собственных значений, собственных векторов, частот и периодов колебаний		STARK_ES
4.5	Распечатать в масштабе формы колебаний, нанести на них значения перемещений.		STARK_ES
4.5	Сравнить компоненты спектров частот и форм колебаний МКЭ с расчетом по программам SERVIK или MathCAD		STARK_ES

 

Литература

1 Строительная механика: Динамика и устойчивость сооружений: Учеб. для строит. спец. вузов / А.Ф.Смирнов [и др.] ; Под ред. Смирнова А.Ф. - М.: Стройиздат, 1984. - 415 с.

2 Дарков, А.В. Строительная механика: учеб. для строит. специальностей вузов / А.В.Дарков, Н.Н.Шапошников. - 9-е изд., испр. - СПб. : Лань, 2004. - 655 с. (1986г.-607 с.)

3 Александров, А.В. Сопротивление материалов. Основы теории упругости и пластичности: Учеб. для строит. специальностей вузов / А.В.Александров, В.Д.Потапов. - 2-е изд., испр. - М.: Высш. шк., 2002.- 399 с.

4  Сенющенков, М.А. Основы устойчивости и динамики сооружений. Учебное пособие для студентов строительных специальностей. – Брянск: РИО БГИТА, 2010. -223с.

5 Сенющенков, М.А. Строительная механика. Динамика и устойчивость сооружений (спецкурс): Методические указания к выполнению РПР №1 "Расчет плоской статически неопределимой рамы с центрально сжатыми стойками на устойчивость методом перемещений" для студентов строительного факультета/ М.А. Сенющенков, С.Н. Швачко. - Брянск, БГИТА, 2009. - 38 с.

6 Швачко, С.Н.  Методические указания к практическим и лабораторным занятиям  "Расчет плоской рамы  с центрально сжатыми стойками на устойчивость в ПК  STARK_ES " для студентов строительных специальностей. -Брянск, БГИТА, 2009 - 7с.

7 Сенющенков, М.А. Строительная механика. Динамика и устойчивость сооружений (спецкурс). Методические указания к выполнению РПР №2 "Динамический расчет многомассовой стержневой системы на собственные и вынужденные колебания" для студентов строительного факультета. -Брянск, БГИТА, 2009 - 88с.

8 Сенющенков, М.А. Использование диалоговой программы интегрирования уравнений движения SERVIK97 в курсе динамики сооружений/ Новые информационные технологии в образовании. -Брянск,  БГТУ, 1998. -С.81.

9 Швачко, С.Н.  Методические указания к выполнению расчетно-проектировочной работы "Динамический расчет многомассовой стержневой системы с использованием ПК  STARK_ES и MathCAD" для студентов дневного обучения строительного факультета. –Брянск: БГИТА, 2010 - 22с.

10 СНиП 2-23-81*. Стальные конструкции. – М.: ГУП ЦПП, 1998. – 96с.

11 СНиП 2.01.07-85*. Нагрузки и воздействия. – М.: ГУП ЦПП, 2001.

12 СНиП 2-7-81* Строительство в сейсмических районах/ Госстрой СССР. – М: АПП ЦИТП, 1991 – 50с.

13 Бате, К.Ю. Численные методы анализа и метод конечных элементов./ К.Ю.Бате, Эд. Вильсон. -М.: Стройиздат, 1982. – 447с.

14 Уилкинсон, Райнш. Справочник алгоритмов на языке АЛГОЛ. Линейная алгебра. – М.: Машиностроение, 1976.

15 Чернов, Ю.Т.   Прикладные методы динамики сооружений (Метод "нормальных форм" и его приложения): Учеб. пособие для вузов по направлению "Стр-во" / Ю.Т.Чернов. - М.: Изд-во АСВ, 2001. - 77с.

16 Коробко, В.И. Строительная механика: Динамика и устойчивость стержневых систем: Учебник / Под ред. В.И.Коробко. – М.: Изд-во АСВ, 2008. – 400с.

17 Даниелов, Э.Р.   Устойчивость и колебания плоских рам: программно-методическое обеспечение по курсу "Устойчивость и динамика сооружений": учеб. пособие для вузов по направлению подгот. дипломир. специалистов "Стр-во" / Э.Р.Даниелов. - М.: Изд-во АСВ, 2004. - 160с.