ОПТИМИЗАЦИЯ УПРАВЛЕНЧЕСКИХ РЕШЕНИЙ В ЭКОНОМИЧЕСКИХ СИСТЕМАХ ЛЕСХОЗОВ
Кривоносов Р.В., Хашир Б.О. (КубГТУ, Краснодар, РФ)
Optimization of administrative decisions in economic systems of timber enterprises.
Управление экономикой предприятий и отдельными его звеньями становится все более затруднительным из-за многообразия возможных производственных и экономических условий и решений, принимаемых на различных уровнях. Особую важность в связи с этим приобретают вопросы научно обоснованного поиска оптимальных решений в различных экономических ситуациях – решений, повышающих эффективность производства и обеспечивающих максимальную прибыль в лесхозах
Решение задач, в которых число неизвестных равно числу связывающих эти переменные уравнений, заключается в решении этой системы уравнений относительно неизвестных переменных. Если число n переменных больше числа r уравнений, то значения r переменных могут быть найдены решением системы уравнений, а остальные m = n – r переменных приходится подбирать так, чтобы их решения наилучшим образом (оптимально) удовлетворяли всем условиям задачи, включая критерии качества ее решения.
Основную задачу математического программирования обычно формулируют следующим образом: найти экстремальное (минимальное или максимальное) значение целевой функции статики
, (1)
соответствующее оптимальным значениям 
оптимизируемых
переменных при ограничениях в виде статических равенств
, l = 1, 2, …, r
и ограничениях в виде неравенств
, j = 1, 2, …, k
Математическое программирование называют линейным, если целевая функция и левые части всех ограничений линейны относительно оптимизируемых переменных.
В этом случае задача численной оптимизации сводится к поиску экстремального значения целевой функции
(2)
при ограничениях-равенствах
,l = 1, 2, …, r (3)
и ограничениях-неравенствах
, j = 1, 2, …, k. (4)
При решении этой задачи число переменных на первом этапе уменьшают, исключив согласно ограничениям-равенствам r, называемых свободными переменными
; l = 1, 2, …, r (5)
и сводят основную задачу линейного программирования к поиску минимума статической целевой функции (1.2)
при ограничениях-неравенствах
, j = 1, 2, …, k
с вычислением на втором этапеr свободных переменных по формуле (5).
В пространстве m оптимизируемых переменных каждой точке с проекциями
на координатные оси
соответствует определенное значение целевой функции. Параллельные плоскостиm-го
порядка (прямые линии при m=2 и гиперплоскости при m>3), на
которых целевая функция постоянна, называют плоскостями равного уровня
Каждому статическому ограничению-неравенству
соответствует граничная плоскость, разделяющая пространство оптимизируемых
переменных на две части, в одной из которых и на граничной плоскости
удовлетворяется это неравенство. Область пространства (многогранник), ограниченная
такими плоскостями, называют областью допустимых решений, а оптимальному
решению соответствует вершина такой области или ее грань, параллельная
плоскости равных уровней целевой функции. Задача линейного программирования и
заключается в отыскании такого оптимального решения, соответствующего оптимальным
значениям
переменных. Если в пространстве переменных нет области, где удовлетворяются все
ограничения-неравенства, то они несовместимы и задача оптимизации неразрешима.
Фактическая связь между параметрами экономической системы, ограничения и целевые функции в точном выражении почти всегда нелинейны. Однако в отдельных случаях нелинейностью можно пренебречь и составить для системы линейную модель, состоящую из линейных алгебраических равенств, неравенств и линейной целевой функции.
Основной идеей линейно-программной модели является рассмотрение производственного плана как составленного из элементарных производственных способов.
Распределительные линейные задачи, используемые при
управлении лесными предприятиями, в том числе и деревообрабатывающими, имеют
характерную формулировку: имеются определенного вида ресурсы Q1, Q2,…,Qi, …,Qmв количествах соответственно b1, b2, …, bi, …, bm. Данные ресурсы необходимо распределить по n
объектам для производства продукции 
. Для изготовления одной
единицы продукции хi, приносящей прибыль Рj
необходимо aij единиц ресурсов Qi.
Расход каждого вида ресурсов для изготовления определенного вида продукции не должен превышать наличия ресурсов:
(6)
Требуется определить, какое количество каждого вида продукции xi надо изготовить, чтобы общая прибыль от реализации продукции была максимальной (известно, что каждый вид продукции может быть реализован в количестве не большем kj единиц), т.е. надо найти такие xi, чтобы целевая функция была максимальной:
(7)
или в краткой записи
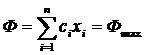(8)
Данная задача разрешима с помощью симплекс-метода, процедура которого состоит из 2-х этапов:
1) проверка плана на оптимальность;
2) включение рентабельных способов и вытеснение из базиса нерентабельных способов
Оптимизация структуры решения экономических задач на конкретном предприятии существенно упрощается при наличии количественных критериев выбора решения на каждом шаге изменения структуры в процессе ее оптимизации. В этом случае, как и при оптимизации параметров любой системы, задача сводится к поиску оптимальных численных значений переменных.
Методы целенаправленного поиска оптимальных решений переменных относят к разделу математики, называемому математическим программированием. Эти методы основаны на составлении вещественной функции оптимизируемых переменных, называемой целевой и принимающей экстремальное значение при оптимальных значениях переменных, что позволяет свести задачу оптимизации переменных к поиску экстремума этой функции.
Задачи нахождения значений оптимизируемых функций
относятся к задачам многомерной оптимизации, которая заключается в поиске
экстремумов функции многих переменных 
. Одним из распространенных методов
многомерной оптимизации является метод координатного спуска Гаусса-Зейделя, который
заключается в поочередном поиске минимума (максимума) по координате х1,
затем х2 и т. д. После нахождения точки минимума по координате х1
переходим к нахождению точки минимума (максимума) по координате х2 и
т.д. Поиск ведется с одинаковым шагом, который уменьшается(увеличивается) после
нахождения всех значений 
.
Основная идея этого метода заключается в том, что поиск точки минимума (максимума) х* сводится к поочередному изменению переменных вдоль одной из координатных осей.
,i=1, 2, …, n, (9)
где li –i-й координатный n-мерный вектор с компонентами:
1, если i=j;
lij =
0 – в противном случае.
Когда длина шага 
на каждой итерации определяется
с помощью одномерной задачи оптимизации
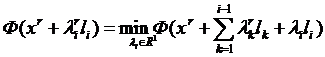, (10)
приходим к методу Гаусса-Зейделя, процедура поиска точки минимума х* в котором сводится к следующей последовательности действий.
1. Задается начальное приближение хr=x0.
2.
Осуществляется циклический
покоординатный спуск из точки хr по формуле (9) с выбором длины шага из условия
(10) для всех i от 1 до n.
Эта процедура образует внутренний цикл, в процессе которого осуществляется одномерная минимизация функции Ф(х) по каждой переменной:
, i=1, 2, …, n
3. После окончания внутреннего цикла в качестве начального приближения х0 принимается точка хnи все вычисления повторяются с п.2.
4. Поиск точки минимума х* заканчивается,
если после очередного внутреннего цикла выполняется условие 
.
Преимущество этого метода для решения задач
оптимизации, заключается в возможности варьирования значениями хi.
Если при использовании симплекс-метода ограничения по хi выглядят
следующим образом , то при использовании метода
Гаусса-Зейделя мы имеем возможность установления ограничений вида 
Причем хmin и xmax устанавливаются в зависимости от условий функционирования исследуемой экономической системы предприятия и позволяют учитывать не только возможности производства и особенности перераспределения ресурсов, но и построить гибкую систему сбыта выпускаемой продукции.