МИНИМИЗАЦИЯ МАССЫ СТЕРЖНЕВЫХ ЭЛЕМЕНТОВ КОРОБЧАТОГО СЕЧЕНИЯ С НАКЛАДКАМИ

 

Моисеев Г.Д. (БГИТА, г. Брянск, РФ)

 

Results of optimisation on weight of box-shaped section with overlays.

 

Одним из основных конструктивных элементов дорожно-строительных машин (ДСМ) являются коробчатые стержни: толкающие брусья бульдозеров, рукояти экскаваторов и прочие элементы. Критерием оптимизации были выбраны их масса или объем при соблюдении условия прочности. Определение оптимальных размеров коробчатого сечения рассмотрено в [1], [2] и  [3]. Однако часто для усиления коробчатого стержня привариваются дополнительные накладки по бокам, а также сверху и снизу.

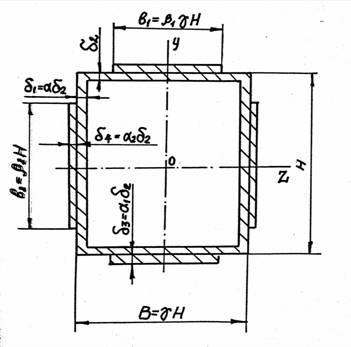
Рисунок - Схема коробчатого сечения с накладками

 

Схема сечения коробчатого стержня с дополнительными накладками приведена на рисунке, где В и Н – соответственно ширина и высота сечения; δ₁ и δ₂ – соответственно толщина вертикальной и горизонтальной стенок сечения; γ = В/H и  α = δ₁/δ₂ – параметры, определяющие форму поперечного сечения; b₁ и b₂ – соответственно длины горизонтальных и вертикальных накладок; δ₃ и δ₄ – соответственно толщины горизонтальных и вертикальных накладок; β₁= b₁/B, β₂= b₂/H, α₁ = δ₃/δ₂, α₂ = δ₄/δ₂ – параметры, определяющие длины и толщины накладок.

В сечении  действуют изгибающие моменты в вертикальной М_y и горизонтальной М_z плоскости, продольная сила N, крутящий момент Т, поперечные силы Q_y и Q_z. Как показывает практика, влиянием поперечных сил при расчете можно пренебречь.

Для вывода зависимостей, непосредственно устанавливающих взаимосвязь параметров стержня коробчатой формы с накладками минимальной массы с параметрами его нагружения, воспользуемся приближенными формулами для определения геометрических характеристик коробчатого сечения с накладками.

Площадь поперечного сечения без накладок А₁ (см. рисунок) определяется по формуле:

А₁ = ВН – bh = ВН – (В - 2δ₁) (Н - 2δ₂),

подставляя значения В = γН и δ₁ = αδ₂, получим

А₁ = 2αδ₂ Н + 2δ₂γ Н - 4αδ₂².

При δ₁ « В и δ₂ « Н величиной 4αδ₂² можно пренебречь. Тогда

А₁ = 2δ₂ Н (γ + α)

Добавляя площади накладок, получим общую площадь сечения 

                           А = 2δ₂ Н (γ + α + β₁ γ α₁ + β₂ α₂)                                 (1)

Аналогично пренебрегая относительно малыми величинами получим приближенные формулы (2)  для определения осевых моментов сопротивления сечения Wz и Wy

 

                                                                           (2)    

Момент сопротивления замкнутого тонкостенного сечения W_k при свободном кручении определим по формуле

W_k = 2 A_kδ_min,

где А_k – площадь, ограниченная средней линией замкнутого контура;

δ_min – минимальная толщина стенок.

Принимая А_k ≈ ВН = γН², получим:

W_k = 2γН²ζδ₂, где ζ = 1 при α ≥ 1 и ζ = α при α ‹ 1.                                  (3)

Найдем зависимости высоты Н поперечного сечения и параметра формы сечения γ = В/Н от действующих в сечении силовых факторов N, M_y, M_z,  T, определяющие минимум интеграла (функционала) объема стержня (2) [3] при соблюдении условия равнопрочности стержня (3) [3] и постоянных по его длине толщинах стенок δ₁ и δ₂.

Функции y_i  размеров поперечного сечения стержня определим как y₁ = γ и y₂ = H.

Используя приближенные зависимости для геометрических характеристик сечения (1) – (3), найдем частные производные ∂/∂H, ∂/∂γ и ∂A/∂H в равенстве (5) [3]. Подставляя значения производных в выражение (6)  [3] и произведя преобразования, получим уравнение экстремали, которое совместно с уравнением равнопрочности образует систему уравнений относительно двух независимых параметров γ  и Н:

 

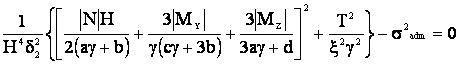,           (4)          

где σ_adm – допускаемые нормальные напряжения металла;

коэффициенты a=1+ β₁ α₁;  b= α+ β₂ α₂;  c=1+ β₁³ α₁;  d= α+ β₂³ α₂.

Система уравнений (4) устанавливает зависимости между геометрическими параметрами сечения и силовыми параметрами, минимизирующие его площадь, а, следовательно, объем и массу стержня.

Полученные зависимости позволяют определить размеры стержней минимальной массы коробчатого поперечного сечения с накладками при соблюдении условия прочности. Предложенный подход применялся при расчете толкающих брусьев бульдозеров, рам автогрейдеров, стрел и рукоятей экскаваторов и других ДСМ. Определяются аналогичные зависимости  для стержней с коробчатым поперечным сечением с внутренними вертикальными диафрагмами.

Литература

1. Анализ качества стержневых систем дорожно-строительных машин. Методы менеджмента качества. / Моисеев Г.Д., Савельев А.Г. – М., 2002. – Вып.11. – С. 40-42.

2. Моисеев Г.Д. Оптимизация сечения элементов стержневых систем дорожно-строительных машин. Конструирование, использование и надёжность машин сельскохозяйственного назначения. Сб. науч. раб./ БГСХА. – Брянск, 2007. – С. 58-66

3. Проблемы строительного и дорожного комплекса: сб. науч. тр. /  Моисеев Г.Д., Савельев А.Г. Минимизация массы стержневых элементов коробчатого сечения.– Брянск: БГИТА, 2008. Вып. 5. – С. 35-39.

4. Гольдштейн Ю.Б., Соломещ М.А. Вариационные задачи статики оптимальных стержневых систем. – Л.:, ЛГУ, 1980. – 208 с.