влияние сортности ламелей на теплопроводность клееного бруса

 

Зайцева К.В., Титунин А.А. (КГТУ, г.Кострома, РФ)

 

In job the influence of a diameter and quantity of knots on heat conductivity of glued beam is proved. The recommendations for designing thickness of protecting designs from клееного of a bar are given in view of it presence of knots.

 

Клееный профилированный брус является высокотехнологичным материалом и постепенно получает широкое применение в современном строительстве. Технология изготовления клееного бруса на сегодняшний день отработана до мелочей. Основные требования к клееной древесине регламентированы рядом нормативно-технических документов [1,2]. На основании этих документов предприятия могут сами разрабатывать технические условия на различные виды клееной продукции.

На этапах проектирования и производства клееного бруса существуют особенности, без учета которых невозможно обеспечить его качество и выполнение эксплуатационных требований, в том числе – касающихся требований по теплозащите. При проектировании теплозащиты обычно используют рекомендации, приведенные в СНиП 23–02–2003, в частности – справочные данные о коэффициенте теплопроводности λ, величина которого для клееного бруса на практике принимается как для цельной древесины. Отличием клееного бруса от цельной древесины является то, что он получается в результате склеивания ламелей, различающихся по количеству и размерам сучков. Ввиду отличий по плотности и направлению волокон, сучки обладают более высокой теплопроводностью. Следовательно, ошибка при проектировании ограждающих конструкций и отклонение от технического регламента производства клееного бруса может привести к увеличению дальнейших затрат на отопление зданий.

Так как для производства бруса используют ламели трех сортов, отличающиеся по количеству и размеров сучков, то для определения влияния сучковатости ламелей на коэффициент теплопроводности всего бруса, необходимо вычислить встречаемость сучков в ламелях каждого сорта. Для этого были проведены необходимые исследования, в частности в ходе натурных измерений пиломатериалов на ООО «ПроДи», г. Кострома определялся диаметр и встречаемость сучков в необрезных пиломатериалах, используемых для производства клееного бруса. Для определения размеров и местонахождения пороков древесины (сучков, трещин, грибных поражений и пр.) определялась ось необрезной доски. Измерение пороков древесины проводилось в направлениях параллельном и перпендикулярном оси доски. Также были замерены расстояния до порока от нижнего торца и от оси («+» в одну сторону, «–» в другую). У каждой доски измерялись длина L и ее ширина в вершинной b и комлевой B частях по наружной пласти. Схема измерения пороков древесины и размеров необрезной доски представлена на рисунке 1.

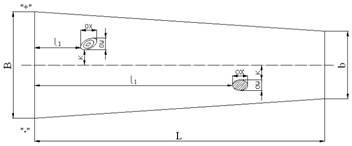
Рисунок 1 – Схема измерения пиломатериалов

 

После измерений пиломатериалы отправлялись на дальнейшую обработку: вырезку дефектных мест в зависимости от дальнейшей сортности и склеивание по длине. Затем подсчитывались средний диаметр и количество сучков на каждом метровом отрезке ламелей по сортам. Результаты по данным исследованиям представлены на рисунках 2–7.

= 10,07 S = 1,32 V = 13,15 % Ss = 0,138 PT = 1,94 %

Рисунок 2 – Гистограмма распределения диаметров сучков в сорте А

= 1,59 S = 1,27 V = 79,76 % Ss = 0,17 PT = 14,83 %

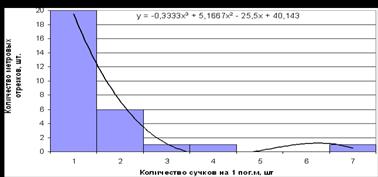
Рисунок 3 – Гистограмма распределения встречаемости сучков

на 1 пог.м длины в сорте А

= 21,95 S = 6,65 V = 30,27 % Ss = 0,21 PT = 1,34 %

Рисунок 4 – Гистограмма распределения диаметров сучков в сорте В

= 2,11 S = 1,101 V = 52,17 % Ss = 0,05 PT = 3,35 %

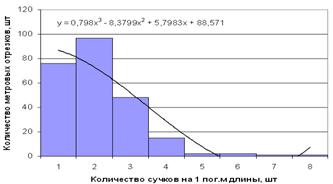
Рисунок 5 – Гистограмма распределения встречаемости сучков

на 1 пог.м длины в сорте В

= 23,41 S = 8,65 V = 36,94 % Ss = 0,25 PT = 1,54 %

Рисунок 6 – Гистограмма распределения диаметров сучков в сорте С

= 2,04 S = 1,02 V = 50,21 % Ss = 0,043 PT = 2,99 %

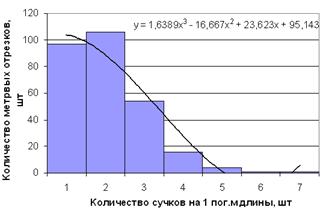
Рисунок 7 – Гистограмма распределения встречаемости сучков

на 1 пог.м длины в сорте С

 

На рисунках 2, 4, 6 представлены гистограммы распределения диаметров сучков на 1 пог.м длины каждого сорта, из которых видно, что в зависимости от сорта наиболее встречаемые диаметры сучков могут доходить до 20–30 мм. Из рисунков 3, 5, 7 видно, что при этом количество сучков в среднем остается 1–3 шт. на 1 пог.м каждого сорта.

Используя приведенные натурные исследования, а также справочные данные и закономерности изменения коэффициента теплопроводности в зависимости от влажности и температуры древесины, направления волокон, была разработана математическая модель для расчета коэффициента теплопроводности клееного бруса, учитывающая диаметр и количество сучков в ламелях, а также число ламелей [3]. В ходе вычислительного эксперимента с использованием данной математической модели были рассчитаны коэффициенты теплопроводности при разных диаметрах сучков и их встречаемости на 1 метре длины. Расчеты представлены в виде диаграммы (рисунок 8).

Рисунок 8 – Диаграмма влияния диаметра и количества сучков на коэффициент теплопроводности клееного бруса

 

Из данной диаграммы видно, что при возрастании объема сучковой древесины, т.е. при снижении сортности ламелей, увеличивается и коэффициент теплопроводности. Для клееного бруса с числом ламелей n = 5 коэффициент теплопроводности может принимать значение в интервале от 0,184 до 0,229 Вт/(м К).

Таким образом, можно сделать следующие выводы:

– значения коэффициента теплопроводности, указанные в        СНиП 23–02–2003 для различных материалов из древесины, применять для клееного бруса не корректно, т.к. в нем присутствуют сучки, значимо повышающие теплопроводность;

– значение коэффициент теплопроводности клееного бруса необходимо применять в зависимости от сорта используемых ламелей, т.е. чем выше сортность ламелей, тем ниже значение коэффициента теплопроводности.

 

Литература

1.        СНиП II–25–80 Деревянные конструкции. – М.: Государственный комитет СССР по делам строительства, 1980. – 27 с.

2.        Технические условия на изготовление стенового клееного бруса (от 3-х ламелей и более). – ТУ «Рамлес», 2007. – 34 с.

3.        Зайцева К.В. Разработка методики определения эксплуатационных  параметров клееного бруса / К.В. Зайцева, А.А. Титунин // Вестник Московского государственного университета леса – Лесной вестник. – 2008. – № 6. – С. 67–71.