К ВОПРОСУ О МОДЕЛИРОВАНИИ ГИСТЕРЕЗИСА В МНОГОСЛОЙНЫХ ВИБРОИЗОЛЯТОРАХ ТРАНСПОРТНОГО МАШИНОСТРОЕНИЯ
Васюков Е.С.1, Пономарев Ю.К.2, Проничев Ю.Н.2
(УК БМЗ 1, г. Брянск, РФ, СГАУ 2, г. Самара, РФ)
In article the question on a correctness of application of the uniform distributed{allocated} squeezing loading between layers of elastic elements is considered{examined} at calculation of a hysteresis vibroinsulators spring type.
Двухслойные балки, работающие на изгиб, успешно используются в качестве упругих элементов в средствах виброзащиты [1 - 3]. Предпосылкой эффективности их использования в технике явилась работа Гудмана и Клампа [4], в которой авторы рассмотрели механизм возникновения гистерезиса в двухслойной консольной балке, деформируемой силой, приложенной на конце консоли и сжатой по длине равномерно распределенной нагрузкой. Распределенная нагрузка в [4] моделировалась в эксперименте конечным числом гибких упругих колец, распределенных по длине и поджатых с двух сторон составной балки.
При использовании двухслойных балок в качестве упругих элементов в средствах виброзащиты создать равномерно распределенную нагрузку по длине пролета практически невозможно. Поэтому для создания хотя бы какой-то сдавливающей нагрузки и обеспечения демпфирующих свойств, применяют предварительное заневоливание балок с приданием их упругим линиям радиусного очертания и последующим полным выпрямлением конструкции силами в специальных обоймах (рис. 1).
Рисунок 1 — Схема выпрямления криволинейных балок
Ранее предполагалось, что в ходе такой технологии на контактных поверхностях балок возникают давления, мало отличающиеся от равномерно распределенных. Для «толстых» балок это действительно так, однако для балок с соотношением толщины к длине менее 0,01, распределенная сдавливающая нагрузка q(z) в основном сосредотачивается на участках, примыкающих к концам балок, и определяется соотношением (рис. 2) [7]:
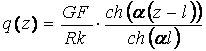, (1)
где G – модуль упругости при сдвиге; F = bh - площадь поперечного сечения балки; R – радиус кривизны ленты; k = 6/5; 2l – длина ленты в распрямленном состоянии,
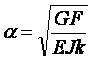, (2)
Е – модуль Юнга, а J=bh3/12- момент инерции поперечного сечения одной балки.
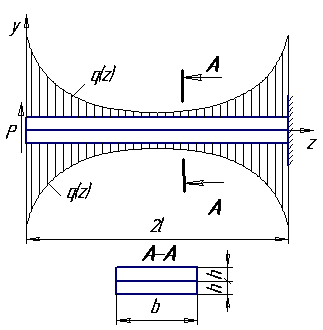
Рисунок 2 — Схема нагружения двухслойной консоли
Вполне очевидно, что использовать модель Гудмана и Клампа [3] для расчета гистерезиса и упругодемпфирующих характеристик в данном случае не корректно. Попытаемся создать математическую модель деформирования двухслойной консоли (рис. 2) с распределенной сдавливающей нагрузкой, определяемой выражением (1) и сравним результаты расчета по ней с расчетами по модели [3].
Рассмотрим процесс циклического деформирования консольной двухслойной балки, сжатой распределенными погонными силами (1) и нагруженной циклически изменяющейся в пределах от –Р до Р сосредоточенной силой Р (рис. 2). При приложении силы Р, в местах контакта двух лент возникают парные силы трения (рис. 3, а)
t(z) = f× q(z), (3)
где f – коэффициент трения.
Перенесем соответствующие силы трения t(z) к оси каждой балки и добавим в соответствии с теоремой Пуансо [5] моменты трения (рис. 3, б), которые будут определяться в виде:
m(z)=t(z)h/2. (4)
Рисунок 3 — Схема распределения сил и моментов трения
Моменты трения, приложенные к каждой балке, направлены в одну сторону и в направлении, препятствующем изменению кривизны балок, следовательно, можно заменить двухслойную балку некоторой эквивалентной балкой с моментом инерции поперечного сечения равным
Jp=2bh3/12, (5)
приложив по всей длине упругой линии момент трения
m0 = ± 2m(z). (6)
При этом на этапе нагружения, когда сила Р направлена вверх, этот момент препятствует изменению кривизны, то есть он направлен против часовой стрелки и является положительным.
На этапе разгрузки, когда сила Р направлена вниз, этот момент препятствует изменению кривизны в противоположном направлении, то есть он направлен по часовой стрелке и является отрицательным. Перемещение балки y в месте приложения силы определим с помощью интеграла Мора:
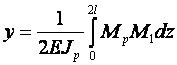, (7)
где Mр – суммарный изгибающий момент от внешней нагрузки и сил трения; M1 – единичный момент:
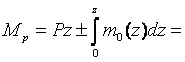
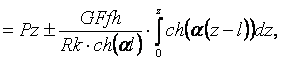(8)
M1=1z. (9)
Подставив аналитические выражения (8) и (9) в интеграл (7), получим:
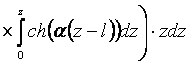. (10)
После интегрирования выражения (10) получим
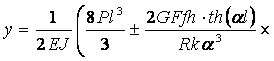
. (11)
Выражение (11) представляет собой внешние ветви петли гистерезиса двухслойной балки, сжатой распределенной нагрузкой (1). При этом важный параметр гистерезиса – обобщенная сила трения T0, определяемая как половина отрезка, отсекаемого нагрузочным и разгрузочным процессами гистерезиса, определяется в виде:
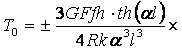
, (12)
а остаточная деформация а0 в виде:
. (13)
Если принять в первом приближении, что на этапах нагружения и разгружения в моменты смены направления деформирования жесткость двухслойной балки определяется нерасслоенным моментом инерции поперечного сечения
J0 = 8bh3/12, (14)
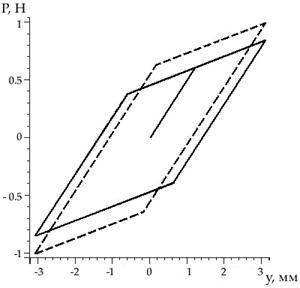
то гистерезис с учетом переменных сдавливающих нагрузок по длине балки будет иметь вид, показанный на рис. 4. Там же показана петля гистерезиса, рассчитанная для равномерной эквивалентной нагрузки, подсчитанной из условия равных площадей под эпюрами неравномерной и равномерной нагрузок q(z).
|
|
y |
||
|
Рисунок 4 — Петли гистерезиса при деформировании двухслойной балки (— переменная сдавливающая нагрузка; - - - равномерная эквивалентная сдавливающая нагрузка) |
Рисунок 5 — Зависимость коэффициента рассеяния от амплитуды перемещения ψ(A) (— переменная сдавливающая нагрузка; - - - равномерная эквивалентная сдавливающая нагрузка) |
Из рис. видно, что обобщенная сила трения при неравномерной нагрузке меньше, чем в модели Гудмана и Клампа [3]. Таким образом, в двухслойных балках с технологией получения сдавливающих нагрузок, показанной на рис. 1, необходимо учитывать неравномерность сил трения по длине.
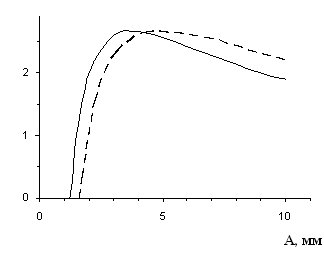
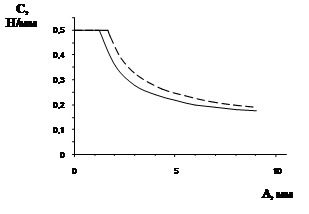
На рис. 5 - 7 показаны результаты обработки полей петель, рассчитанные двумя методами: разработанным в настоящей работе и методом Гудмана и Клампа. Здесь рассеянная циклическая энергия W численно равна площади петли гистерезиса [6], среднециклическая жесткость С и коэффициент поглощения y подсчитывались по формулам:
C=Pmax/A, (15)
y=2W/APmax, (16)
где Pmax – амплитуда силы; А – амплитуда перемещения.
|
|
|
|
Рисунок 6 - Зависимость рассеянной энергии от амплитуды перемещения W(A) (— переменная сдавливающая нагрузка; - - - равномерная эквивалентная сдавливающая нагрузка) |
Рисунок 7 - Зависимость среднециклической жесткости от амплитуды перемещения C(A) (— переменная сдавливающая нагрузка; - - - равномерная эквивалентная сдавливающая нагрузка) |
Таким образом, видно, что максимальное значение коэффициента рассеяния для двухслойной балки определенное 2 методами составляет ψ = 2,66. В нашем случае максимум ψ(A) смещается в сторону меньших амплитуд перемещения. Расчет по методу Гудмана и Клампа дает завышенные значения рассеянной энергии практически во всем диапазоне амплитуд перемещения.
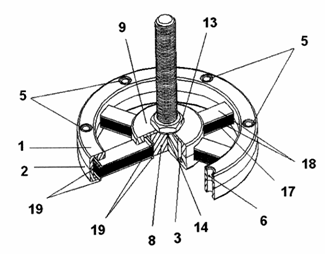
Рисунок 8 — Конструкция виброизолятора с использованием заневоленных лент радиусного очертания
Весьма интересно отметить, что в задаче Гудмана и Клампа обобщенная сила трения численно равна распределенному по длине суммарному моменту сил трения m0 (6). В нашем случае эта величина определяется выражением (12) и, кроме f, h, b, E, G и l , зависит от радиуса R. Кроме того, несмотря на то, что, на большей части контакта слоев давление практически отсутствует, рассмотренная упругодемпфирующая система обладает неплохими демпфирующими характеристиками, что дает надежду использования таких элементов в конструировании цельнометаллических виброизоляторов.
В качестве одного из вариантов использования изложенных теоретических результатов, приведем конструкцию цельнометаллического виброизолятора, показанную на рис. 8.
Виброизолятор состоит из двух соосно расположенных разъемных обойм, имеющих вид тел вращения. Наружная обойма состоит из двух оппозитно состыкованных друг с другом одинаковых фасонных колец 1, 2, в каждой из которых выполнены один кольцевой паз 3 и не менее трех радиальных пазов 4, которые служат для установки в них многослойных упругодемпфирующих элементов с конструкцией, подробно показанной на рис. 9.
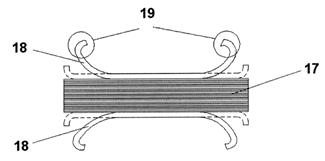
Рисунок 9 - Конструкция упругодемпфирующих пакетов
Элемент состоит из набора лент одинаковой толщины и ширины 17, с двух сторон сжатых более толстыми накладками 18, имеющими на рабочей части радиусный профиль, а на концах – отгибные усики 19. После установки пакетов в обоймы, профилированные накладки распрямляются, создавая между слоями пакетов распределенную сдавливающую нагрузку [8], определяющую уровень демпфирующих свойств устройства.
Литература
1. Вибрации в технике: Справочник в 6-ти т./Том 6. - Защита от вибрации и ударов/Под ред. К.В. Фролова. - М., Машиностроение, 1981. – 476 с.
2. Пановко Я.Г. Внутреннее трение при колебаниях упругих систем. -М.: Физматгиз, 1960. – 190 с.
3. Конструкционное демпфирование в неподвижных соединениях/ Под ред. Н.Г.Калинина. – Рига: изд-во АН Латв. ССР, 1960. – 220 с.
4. Goodman L.E., Klump J.H. Analysis of Slip Damping. Journ. of Appl. Mech., № 3, 1956.
5. Тарг С.М. Курс теоретической механики. -М.: Физматгиз, 1963.
6. Чегодаев Д.Е., Пономарев Ю.К. Демпфирование. – Самара: Изд-во СГАУ, 1997. – 334 с.
7. Феодосьев В.И. Избранные задачи и вопросы по сопротивлению материалов. Издание четвертое, исправленное и дополненное. -М., Наука, 1973. – 400 с.
8. Сойфер А.М., Эскин И.Д. Поперечный изгиб многослойной консоли. В сб. «Вибрационная прочность и надежность авиационных двигателей. Труды КуАИ, вып. 19. –Куйбышев. -С.335 – 345.