НЕКОТОРЫЕ МЕТОДЫ АНАЛИЗА КОНСТРУКТОРСКИХ РЕШЕНИЙ
Шахнюк Л.А. (БГИТА, г. Брянск, РФ)
The question of optimum designing of designs of drives of cars and mechanisms is considered.
На каждой стадии проектирования варианты решения подвергаются анализу с целью выбора того из них, который в наибольшей степени удовлетворяет требованиям технического задания. Рассмотрим два метода анализа конструкторских решений.
АНАЛИЗ И СРАВНЕНИЕ БЛОК – СХЕМ И КИНЕМАТИЧЕСКИХ СХЕМ МАШИН И МЕХАНИЗМОВ
На стадии технического предложения и эскизного проектирования удобно сравнивать блок – схемы или кинематические схемы машин и механизмов с целью определения лучшей при условии обеспечения высокой надежности, унификации, технологичности и т. д. Рассмотрим использование этой методики на примере привода ленточного конвейера.
Представим себе, что в процессе разработки вариантов привода ленточного конвейера для перемещения мебельных деталей получены следующие кинематические схемы (рисунок 1).
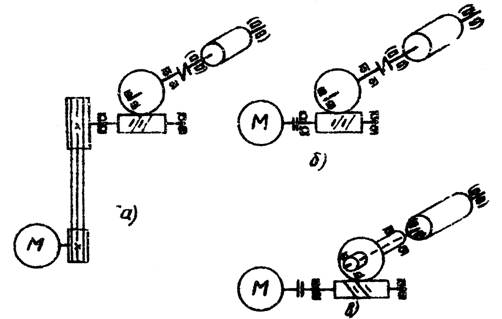
Рисунок 1 – Варианты кинематических схем привода ленточного конвейера
Каждая из них имеет определенные достоинства и недостатки. Схема (рисунок 1а) удобна с точки зрения размещения двигателя под рамой конвейера, ременная передача предохраняет двигатель от перегрузки и не требует введения в конструкцию привода элементов, обеспечивающих точность установки двигателя по отношению к приводному валу. Однако, учитывая значительный диапазон передаточных чисел, реализуемых в червячной передаче, а также возможность применения фланцевых двигателей, жестко соединяемых с редуктором через центрирующий элемент, схема (рисунок 1б) кажется более рациональной. Конструкция муфты, соединяющей двигатель и редуктор, упрощается, так как становится возможным применение простой втулочной муфты. Сложность центрирования редуктора по отношению к приводному валу конвейера остается неизменной.
Поскольку речь идет о приводе к ленточному конвейеру, то предохранение привода от перегрузки осуществляется самой лентой, проскальзывающей относительно барабана, и это является дополнительным стимулом к отбраковке первого варианта.
В третьем варианте (рисунок 1в) вопрос центрирования привода по отношению к приводному валу решается более просто, чем во втором варианте, так как комплекс из двигателя и редуктора, соединённых жестко друг с другом, навешивается на приводной вал, а передача момента осуществляется с помощью зубчатого (шлицевого) соединения. Отпадает необходимость проектировать и изготавливать раму привода. Число элементов цепи «двигатель – приводной вал» значительно сокращается, что позволяет повысить надежность привода в целом. Однако этот вариант применим только при небольших мощностях, так как приводит к значительным консольным нагрузкам массы на приводной вал. При больших мощностях второй вариант предпочтительнее.
Тем не менее, возникающие в этом варианте консольные нагрузки на приводные валы от неточного центрирования достаточно велики.
Заключая такой анализ, следует, видимо, отдать предпочтение второму и третьему вариантам, оставив их для дальнейшей проработки. Если же эти варианты не устраивают по каким – либо причинам, то необходимо продолжить работу по выработке новых, сочетая, например, первый и третий варианты или выйдя за пределы схем с червячным редуктором.
Нетрудно видеть, что анализ ведется с опорой на некоторые критерии. В рассматриваемом случае в качестве таких критериев используются надежность (чем меньше элементов в последовательной цепи, тем выше надежность) и эффективность (степень унификации, технологичность,0 материалоемкость). Безусловно, такой анализ индивидуален, субъективен. Тем не менее, он практикуется и может быть рекомендован для анализа систем.
МЕТОД ОПТИМИЗАЦИИ ПРОЕКТНЫХ РЕШЕНИЙ
Разработка конструкций машины или механизма на более поздних стадиях проектирования дает возможность провести анализ вариантов по количественным показателям стоимости и массы. Пример такого анализа рассмотрен на сравнении вариантов конструкции привода ленточного конвейера.
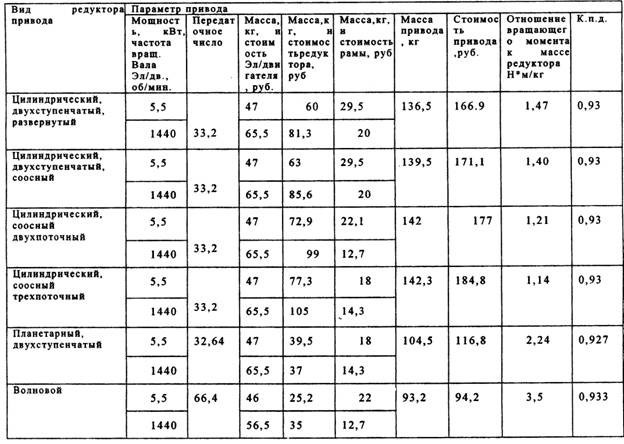
В таблице 1 приведены данные по сравнению рассматриваемых вариантов конструкции. Как видно из таблицы, в пределах принятых вариантов следует отдать предпочтение двум вариантам: планетарному и волновому редуктору. Однако, вариант с волновым редуктором следует оценить еще раз с точки зрения технологичности, степени сложности конструкции, надежности в работе. С другой стороны, если оба варианта не устраивают конструктора по каким – либо причинам, то следует рассмотреть и другие варианты привода.
Таким образом, постепенно переходя от качественных к количественным критериям сравнения, можно с все более возрастающей точностью выполнить технико-экономический анализ вариантов. Однако, при таком анализе лучший вариант является относительно лучшим. Чтобы этот или какой – либо другой вариант стал действительно лучшим, оптимальным, необходимо при разработке каждого найти и использовать все возможности расчетно-конструкторского, технологического, исследовательского и эксплуатационного характера, иными словами, в рамках разработки конкретного варианта конструкции машины конструктор должен найти оптимальное решение. Только после этого сопоставление нескольких вариантов позволит установить самый лучший из них.
Таблица 1 – Сравнение вариантов конструкции привода ленточного конвейера

Под оптимальным решением принято принимать такое, которое позволяет определить минимум или максимум некоторой величины (называемой критерием или целевой функцией качества) при заданных ограничениях.
Для машинной техники в общем плане оптимизируемой величиной (критерием) являются материальные затраты (их минимум) на производство и эксплуатацию при условии (ограничении) выполнения требований задания на проектирование. Возможным критерием оптимальности может приниматься максимум эффективности машины при определенных затратах. Пример оптимального многоступенчатого редуктора рассмотрен в работе [3].
Литература
- Джонс Дж. Методы проектирования (перевод с английского) – М., Мир, 1986 г. – 326 с.
- Шахнюк Л.А., Тихомиров В.П. Детали машин. Технология проектирования. -Брянск, 2001. – 334 с.
- Шахнюк Л.А. Оптимальное проектирование многоступенчатых редукторов. Актуальные проблемы лесного комплекса. Вып. №1. -Брянск, 2005.