МИНИМИЗАЦИЯ МАССЫ СТЕРЖНЕВЫХ ЭЛЕМЕНТОВ КОРОБЧАТОГО СЕЧЕНИЯ

 

Моисеев Г.Д. (БГИТА, г.Брянск, РФ), Савельев А.Г. (МАДИ, г.Москва, РФ)

 

The result of optimisation of the box-shaped section cores of the minimum weight is considered.

 

Машины лесного комплекса имеют рабочие органы, связанные с тяговым или энергетическим средством стержневыми системами коробчатого тонкостенного сечения, например: стрелы, рукояти, толкающие брусья. Одним из основных показателей качества стержневых систем является их металлоемкость при соблюдении условий прочности.

Масса стержневой системы

                                            ,

где V -  объем; ρ – объемная масса, для стали ρ=const.

Критерием оптимизации при ресурсосбережении может быть выбран минимум объема стержневого элемента при выполнении условия прочности.

Схема коробчатого поперечного сечения приведена на рисунке 1, где В и Н – соответственно ширина и высота сечения; δ₁ и δ₂ – соответственно толщина вертикальной и горизонтальной стенок сечения; γ = В/H и α = δ₁/δ₂ – параметры, определяющие форму поперечного сечения.

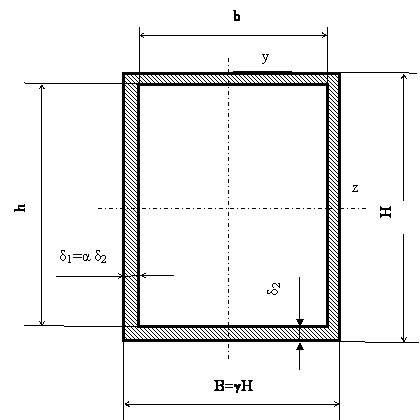
Рисунок 1 – Схема коробчатого сечения

 

В работе [1] исследовалась взаимосвязь между параметром сечения γ с постоянной толщиной стенок (δ₁=δ₂=const) и силовыми факторами, действующими в сечении, при косом изгибе.

Для этого случая было получено уравнение экстремали:

                               ,                                                     (1)

где М_y, М_z – изгибающие моменты в сечении, действующие относительно осей y и z.

Решая уравнения экстремали при известных величинах М_y и М_z, , получим значение параметра γ, определяющего форму сечения минимальной массы. Величины Н и В = γН могут быть получены из условия равнопрочности, записанного для данного сечения. Однако, кроме изгибающих моментов М_y, М_z, в сечении обычно действуют продольная сила N и крутящий момент Т.

При определении оптимальных размеров стержня необходимо учитывать влияние различной толщины стенок δ₁ и δ₂ на форму поперечного сечения и массу.

Определим объем стержня

,                                                                                     (2)

где x₁ и x₂ – пределы интегрирования, взятые по координате х, направленной вдоль продольной оси стержня; А – площадь поперечного стержня; y_i (x) – некоторая задаваемая функция i-x размеров сечения от координаты х, которой могут быть размеры сечения В, Н и толщина стенок δ_i, а также соотношения этих размеров.

Минимум массы стержня может быть достигнут только при соблюдении условия его равнопрочности, которое в угловых точках сечения по третьей теории прочности [2]

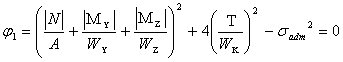
,                                   (3)
где W_y , W_z, W_k – соответственно моменты сопротивления сечения при изгибе в двух взаимно перпендикулярных плоскостях и кручении; Т – крутящий момент; σ_adm – допускаемые нормальные напряжения.

Функции Y_i, реализующие экстремум определенного интеграла (2) при условии равнопрочности (3), определяются из системы уравнений Эйлера [3]

 

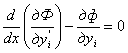                _,                                                                                                 (4)

    m

где Ф – целевая функция, Ф = А + ∑   λ_k φ_k,

    k=1

i =  1, 2, …, n;   n – число искомых параметров сечения;

m – число дополнительных условий; λ_k – неопределенные множители Лагранжа; φ_k – k-е дополнительное условие.

В нашем случае на величины, входящие в выражение (2), наложено одно условие равнопрочности (3), то есть m = 1.

Система уравнений (4) при m = 1 преобразуется после подстановки значения Ф и последующего дифференцирования по Y_i в систему n равенств

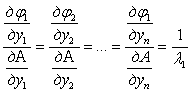
(5)

Подставив значение φ_k в (5) и проведя необходимые преобразования, получим при числе искомых параметров сечения n = 2

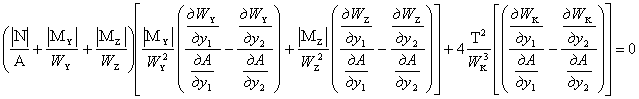                                                                                                                                                                                                  (6)

Уравнение (6) устанавливает параметры, минимизирующие объем и массу стержня, общие зависимости между функциями размеров сечения Y₁ и Y₂ и силовыми факторами, действующими в сечении.

Площадь поперечного сечения А определяется по формуле:

А = ВН – bh = ВН – (В - 2δ₁) (Н - 2δ₂),

подставляя значения В = γН и δ₁ = αδ₂, получим

А = 2αδ₂ Н + 2δ₂γ Н - 4αδ₂².

При δ₁ « В и δ₂ « Н величиной 4αδ₂² можно пренебречь. Тогда

А = 2 Н δ₂ (γ + α)                                                                                                              

;                                                                 (7)
        Момент сопротивления замкнутого тонкостенного сечения W_k при свободном кручении определим по формуле, приведенной в  [2]:

W_k = 2 A₁δ_min,

где А₁ – площадь, ограниченная средней линией замкнутого контура;

δ_min – минимальная толщина стенок.

Принимая А ≈ ВН = γН², получим

W_k = 2γН²δ₂     при α  ≥ 1;

W_k = 2γН²δ₂α  при α ‹ 1.

Тогда W_k = 2γН²ζδ₂, где ζ = 1 при α  1 и ζ = α при α ‹ 1.                              (8)

Найдем зависимости высоты Н поперечного сечения и параметра формы сечения γ = В/Н от действующих в сечении силовых факторов N, M_y, M_z и  T, определяющие минимум интеграла объема стержня (2) при соблюдении условия равнопрочности стержня (3).

Функции размеров поперечного сечения Y_i определим как y₁ = γ, y₂ = H.

Используя приближенные зависимости для геометрических характеристик сечения (7,8), найдем частные производные в равенстве (5).

Подставляя значения производных в выражения (5,6) и, произведя преобразования, получим уравнение экстремали (9), которое совместно с уравнением равнопрочности (10) образует систему двух уравнений относительно двух независимых параметров γ  и Н

 

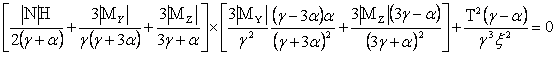  (9)
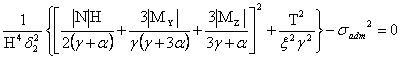                                             (10)

Система уравнений (9,10) устанавливает минимизирующие объем и массу стержня зависимости для каждого сечения по длине стержня между высотой сечения Н и параметра формы γ от действующих в сечении силовых факторов N, M_y, M_z и T. Полученные зависимости позволяют определить размеры стержневого элемента конструкции лесных машин минимальной массы с коробчатым тонкостенным поперечным сечением при соблюдении условия прочности.

При действии в сечении отдельных силовых факторов имеем следующие частные случаи [4]:

1. В сечении действует только продольная сила N. Уравнение экстремали (9) принимает вид тождества 0 = 0. В этом случае оптимума сечения по параметру формы γ нет.

2. В сечении действует только крутящий момент Т. Условие оптимальности сечения из уравнения экстремали принимает вид:

γ – α = 0 или γ = α, или В / Н = δ₁ / δ₂.

3. В сечении действует только один изгибающий момент М_y или М_z. В первом случае условие оптимальности γ - 3α = 0 или γ = 3α, во втором случае 3γ – α = 0 или γ = α/3.

4. В сечении действуют изгибающие моменты М_y и М_z. Уравнение экстремали принимает вид уравнения (1), решая которое определим оптимальный параметр формы сечения γ. Интервал, в котором находится решение γ Є [1/3, 3].

 

Литература

1. Софронов Ю.Д. Об оптимальной форме поперечного сечения при косом изгибе. Оптимальное проектирование конструкций / Труды/КАИ,1975, вып.189.-С.36-42.

2. Дарков А.В., Шапиро Г.С. Сопротивление материалов: Учебник для вузов. – М.: Высшая школа, 1975. – 654 с.

3. Гольдштейн Ю.Б., Соломещ М.А. Вариационные задачи статики оптимальных стержневых систем. – Л.: ЛГУ, 1980. – 208 с.

4. Савельев А.Г., Моисеев Г.Д. Анализ качества стержневых систем дорожно-строительных машин// Методы менеджмента качества. -2002. - №11.