РАЗРАБОТКА ТРОСОВЫХ ВИБРОИЗОЛЯТОРОВ С ЛИНЕЙНЫМИ ХАРАКТЕРИСТИКАМИ

 

Мелентьев В.С., Гвоздев А.С., Пономарев Ю.К. (СГАУ, г. Самара, РФ)

 

Abstract: The objective of work consist in development of mathematical model of all-metal filters with elastic elements of regular structure. In the given work the mathematical model develops with reference to a subset cable all-metal filters with linear characteristics. For verification of the developed model a designing linear metal filter has been carried out.

 

Одной из главных тенденций развития ведущих отраслей промышленности, в том числе строительного и дорожного комплексов, по-прежнему остается продление жизненного цикла изделий путем повышения надежности. Так как наиболее частой причиной отказов являются вибрационные и ударные нагрузки на оборудование в процессе работы, то перспективным направлением в этом плане можно считать разработку и применение новых типов виброизоляторов. Данная статья посвящена методике проектирования тросового виброизолятора, обладающего рядом преимуществ по сравнению с виброзащитными устройствами другого типа.

 

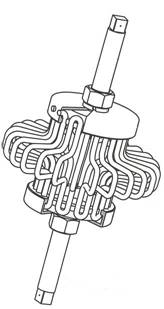
Предлагаемый виброизолятор[1] относится к области машиностроения, в частности, к упругим демпфирующим элементам, и может быть использован для защиты приборов, агрегатов и оборудования от перегрузок, ударов и вибрации в любой области техники (рис. 1). С точки зрения конструкции, устройство представляет собой две одинаковые обоймы, соединенные между собой ансамблем рабочих элементов троса, выполненные в виде чередующихся по окружности обойм радиусных участков. Техническим результатом, на достижение которого направлено создание данной модели виброизолятора, является обеспечение высокой надежности виброударозащиты и получение равножесткостной линейной характеристики по трем взаимно перпендикулярным направлениям, позволяющей

Рисунок 1 – Тросовый виброизолятор

исключить возникновение суб- и супергармонических резонансов в рабочей зоне частот виброзащитной системы.

 

 

 

Это достигается тем, что в известном виброизоляторе, состоящем из двух разъемных обойм в виде тел вращения, каждая из которых, в свою очередь, состоит из двух частей, сопрягаемых друг с другом вдоль цилиндрических поверхностей и отрезков троса, упруго соединяющего обе обоймы, пакет рабочих элементов троса выполнен в виде последовательно соединенных друг с другом, чередующихся прямолинейных и радиусных участков троса. Причем два прямолинейных участка на концах рабочих элементов троса защемлены в обоймах, один средний прямолинейный участок выполнен с осью, параллельной концевым, а два других прямолинейных участка перпендикулярны трем первым.

Принципиальным отличием представленного варианта виброизолятора является следующее. За счет того, что упругий элемент выполнен в виде симметричного пространственного троса осуществляется выполнение равножесткостной линейной характеристики по трем взаимно перпендикулярным направлениям, что, в свою очередь, позволяет исключить возникновение суб- и супергармонических резонансов в рабочей зоне частот виброзащитной системы.

 

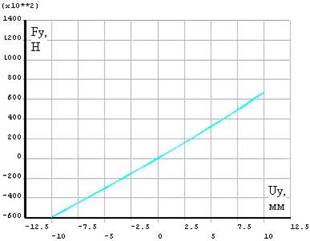
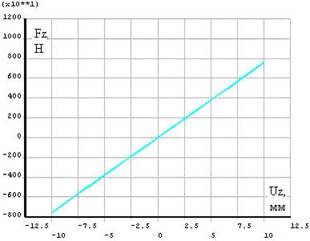
а) по оси	б) в боковом направлении
Рисунок 2 - Нагрузочные характеристики виброизолятора

 

Виброизолятор работает следующим образом. При действии вертикальной нагрузки вибрационного или ударного характера витки тросового элемента деформируются, компенсируя действие приложенных нагрузок и диссипируя их энергию. Так как тросовые элементы равномерно расположены по окружности, то устойчивость виброизолятора в горизонтальном направлении будет выше, чем у прототипа.

Теоретическое исследование, проведенное авторами статьи, показало, что виброизолятор способен обеспечить заданный уровень стабильности характеристик, а конструкция в целом способна поддержать эти характеристики в неизменном состоянии в процессе работы.

 

В плане теоретического обоснования конструкции данного виброизолятора необходимо отметить следующие основные моменты. Во-первых, математическая модель условно была разбита на две части: модель виброизолятора и модель упругодемпфирующего элемента. Во-вторых, модель виброизолятора описывает граничные условия закрепления линии троса и геометрию объекта. В данной модели одиночный элемент рабочего участка троса описан следующим образом (см. рисунок 3) где а и b – прямолинейные участки троса, r – радиусные участки троса, Р – возбуждающая сила.

Рисунок 3 - Рабочий участок троса

 

В-третьих, модель упругодемпфирующего элемента была создана на базе КЭ-комплекса ANSYS, где был определен набор параметров, описывающих упругогистерезисные характеристики элемента и виброизолятора в целом [1]:

- модуль упругости материала Е, Н/м²;

- коэффициент Пуассона  m;

- параметры, определяющие конструкцию поперечного сечения элемента: число проволок  n, диаметр проволок d_i, м, моменты инерции сечения относительно осей x и z – Jx, Jz .

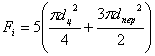                                                                                  (1)            

- площадь поперечного сечения упругого элемента, м²,

где d_ц и d_пер – диаметры центральной и периферийной проволочек, соответственно;

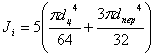                                                                                  (2)       

- момент инерции поперечного сечения упругого элемента, м⁴;

                                                                                                              (3)

- эквивалентный радиус упругого элемента, м.

Была построена упругая линия, выбран тип конечного элемента (BEAM4), проведена разбивка на конечные элементы и заданы кинематические и динамические граничные условия исходя из параметров рассматриваемой конструкции. Была установлена опция нелинейного анализа системы при деформации (NLGEOM) и проведен расчет, в ходе которого были определены нагрузки, соответствующие заданным деформациям в трех взаимно перпендикулярных направлениях y (ось виброизолятора), x и z. Полученные характеристики были представлены в размерном и безразмерном виде. 

Аналитические выражения для расчета безразмерных нагрузочных характеристик элемента виброизолятора имеют вид:

                                                                                              (4)               i = x, y, z;

- безразмерная нагрузка;

где  - безразмерная деформация, коэффициенты с_ij приведены в таблице 1.

Таблица 1 – Коэффициенты для расчета нагрузочных характеристик

j®	1	2	3	4
cxj	0,381	-0,0729	0,0599	-0,00953
cyj	0,381	-0,0729	0,0599	-0,00953
czj	0,988	-0,8660	0,4690	-0,09260

Таким образом, чтобы рассчитать упругую нагрузочную характеристику элемента в направлении соответствующей оси, необходимо воспользоваться обратным преобразованием

                                                                                        (10)

- нагрузка на виброизолятор, Н;

                                                                                         (11)

- деформация, м.                  

Здесь, как и ранее, под индексами i подразумеваются индексы x, y и z.

Определив производную от соответствующей нагрузочной характеристики, пронормировав ее по начальному значению, а затем экспериментально, найдя обобщенную силу трения Т, можно рассчитать поле петель гистерезиса. При этом можно воспользоваться либо упрощенными формулами, либо моделью трения Чегодаева – Пономарева с плавными обводами петель гистерезиса  в виде (подробнее о построении математической модели см. [1]):

                                           (12)

- обобщенная сила трения, Н.

Успешное моделирование виброизолятора предложенной конструкции показывает применимость разработанного алгоритма для расчета тросовых виброизоляторов для нужд строительного и дорожного комплексов.

 

Литература

1. Пономарев Ю.К., Калакутский В.И. Многослойные цельнометаллические виброизоляторы с упругими элементами регулярной структуры. – Самара: Изд-во СГАУ, 2003. – 198 с.

2. Патент РФ №2199683 МПК F16F 7/14. Способ изготовления упругофрикционных элементов тросовых виброизоляторов / Пономарев Ю.К., Архангельский С.В., Гунин В.А. и др. Заявл. 24.11.00, опубл. 27.02.03 Бюл. №6.