ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПЕРЕДАЧИ ЧЕРЕЗ СТЕНКИ РЕЗЕРВУАРОВ ГАЗОВЫХ СИСТЕМ

 

Лазарев В.В. (БГИТА, г. Брянск, РФ)

 

On the grounds of equations first begin thermodynamicses are received functional dependencies for determination of the factor heat issue, as functions of the factors politropa processes of the filling and outflow of the gas from reservoir.

 

Определение величины коэффициента  к теплопередачи через стенки резервуаров по известным зависимостям представляет из себя сложную и громоздкую задачу, поскольку она является функцией большого числа факторов.

Ниже приведен вывод формулы для определения  К в  политропических процессах наполнения и истечения газов из резервуаров.

Для вывода расчетных зависимостей примем за исходное уравнение первого начала термодинамики для процесса одновременного наполнения и истечения газа из резервуара переменного объема. Исходное уравнение, представленное в дифференциальной форме, запишем в следующей форме

,              (1)

где  и   – удельное теплосодержание соответственно входящего                       и выходящего газа;  и  – секундные расходы соответственно входящего и                       выходящего газа; t – время процесса; – количество тепловой энергии, полученное или отданное газом в резервуаре вследствие его теплообмена с окружающей средой за время dt;  и  – изменение внутренней энергии газа в резервуаре и его объема за время dt.

С учетом того, что

,

 

,

 

,

,

 уравнение (1) после преобразований примет следующий вид

 

.

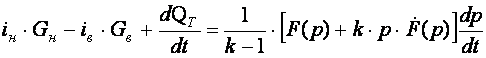Откуда

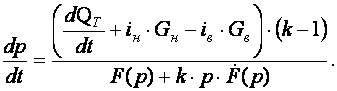                        (2)

где  k – показатель адиабаты.

Представим значение   в следующем виде

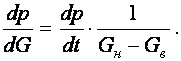                                                                            (3)

Производную , входящую в зависимость (2), на основании формулы Ньютона можно представить как       

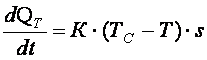                       ,                                     (4)

где К – коэффициент теплопередачи от газа в резервуаре в окружающую среду; Т и Т_С – температуры соответственно газа в резервуаре и окружающей среды; s – поверхность теплообмена резервуара.

Тогда после совместного решения этих  уравнений получим

 

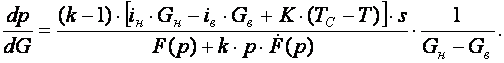    (5)

Подставив в зависимость (5) значения 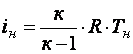 (Т_н – температура газа, поступающего в резервуар) и 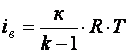, а также заменив ,  после ряда преобразований получим

 

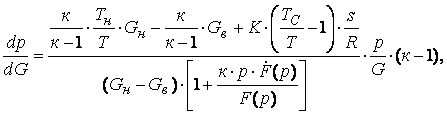            (6)

 

где к – показатель адиабаты.

Имея в виду, что 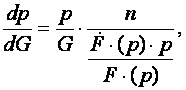    то на  основании зависимости (6) получим

,

где п – показатель политропы.

Откуда

    (7)

Для случая, когда происходит процесс одновременного наполнения и истечения газа из резервуара постоянного объёма (V = F(p) = const, )

                              (8)

Тогда для случая наполнения газом резервуара постоянного объёма ()

,                                     (9)

а для случая истечения газа из резервуара постоянного объема (G_н = 0)

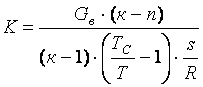.                                     (10)

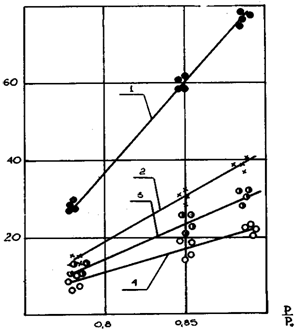
На рисунках приведены значения коэффициента теплопередачи при  истечении  воздуха  из  шины 16.00-20  модели  И-159  ГОСТ 17393–72 (V = 0,37 м³) и из стального резервуара объемом V = 0,27 м³ (толщина стенки - 6 мм) с использованием опытных данных Т и n.

 

      – стальной  резервуар, насадок с эффективным проходным сечением,    

           м²;

      – шина 16.00-20, вентиль  м²;

     – стальной резервуар, насадок  м²;

     – стальной резервуар, насадок  м².

 

Рисунок 1 - Опытные значения коэффициента теплопередачи при                          истечении воздуха из резервуара постоянного объёма.

 

Из рисунков 1  и 2  видно, что величина К существенно зависит не только от материала стенок резервуара, а и от интенсивности процесса истечения (отношения давлений  и эффективной площади проходного сечения насадка ).

 

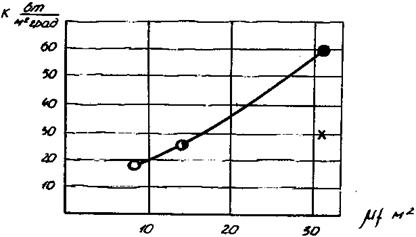
Рисунок 2- Зависимость коэффициента теплопередачи от величины эффективного проходного сечения насадка при истечении воздуха из резервуара при  = 0,85 (обозначения те же, что и на рисунке 1)

 

Полученные функциональные зависимости  позволяют определять текущее значение коэффициента теплопередачи через стенки резервуаров технических систем, связанных с перетеканием газов, а также уровень интенсивности его изменения в зависимости от пропускной способности газопроводов.

Для этой же цели предлагаемые зависимости могут быть использованы для оценки теплового состояния шины пневматического колеса в зависимости от толщины его протектора и пропускной способности вентиля шины.

Литература

1. Бронштейн, И.Н. Справочник по математике для инженеров и учащихся вузов/ И.Н. Бронштейн, К.А. Семендеев. – М.: Наука, 1980. – 976 с.

2. Герц, Е.В. Динамика пневматических приводов машин автоматов./ Е.В. Герц, Г.В. Крейнин. – М.: Машиностроение, 1985. – 272 с.

3. Дрыжаков, Е.В. Техническая термодинамика./ Е.В. Дрыжаков, С.И.Исаев, И.А. Кожинов и длр.-М.: Высшая школа, 1981. – 438 с.