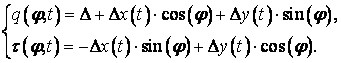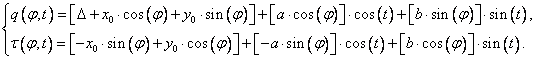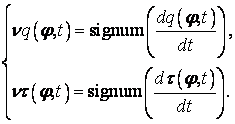ТРАНСФОРМАЦИЯ ГИСТЕРЕЗИСА В КОЛЬЦЕВОМ ДЕМПФЕРЕ
ИЗ МАТЕРИАЛА МР ПРИ ИЗМЕНЕНИИ ПАРАМЕТРОВ
ЭЛЛИПТИЧЕСКОЙ ТРАЕКТОРИИ ДВИЖЕНИЯ ЦАПФЫ

 

Спивак С.Е., Пономарёв Ю.К. (СГАУ, г. Самара, РФ)

 

Materials of theoretical investigation of hysteresis transformation mechanisms in dry friction ring dampers from material MR are presented.

В последнее время сильно возросло внимание исследователей к теоретическим проблемам гистерезисных систем. И, хотя работ по статике и динамике гистерезисных систем довольно много, ещё остается много белых пятен в этом вопросе.

Фойгт [1] еще в 1898 году высказал гипотезу о том, что силы внутреннего трения в материалах носят вязкий характер, то есть гистерезис в координатах напряжение-деформация () представляется зависимостью эллиптического вида. На какое-то время та гипотеза вошла в практику инженерных расчетов.

Однако у ряда исследователей возникли сомнения. Было замечено, что модель Фойгта не в состоянии отобразить релаксацию – существенное свойство реальных материалов. Появились модели Максвелла, Пойнтинга-Томпсона [4]. Указанные модели были созданы также на упруго-вязких схемах, что приводило к зависимости рассеянной энергии от частоты. У реальных материалов такая зависимость отсутствует.

Впервые оригинальные математические модели гистерезиса при растяжении гибкой полосы и при изгибе двухслойной балки дали Пиан и Халловелл [2], Гудман и Кламп [3,4].

В рамках этих моделей было показано, что рассеяние энергии в многослойных системах значительно превосходит внутреннее трение в материалах. Были найдены оптимальные режимы сдавливания слоев, при котором обеспечивается максимум рассеяния энергии. Эти результаты явились мощным толчком к исследованию упругогистерезисных систем и их использованию в виброзащитной технике [2,4,5,6].

В 80-х годах прошлого века было найдено ещё одно свойство механических диссипативных систем – зависимость формы гистерезиса от вида траекторий движения [5]. Было доказано, что при однонаправленном деформировании упругодемпфирующего устройства петли гистерезиса имеют форму со скачкообразным изменением жёсткости в точках смены знака скоростей движения. При движении подвижной точки упругодемпфирующего устройства по замкнутой круговой траектории форма гистерезисных петель становится эллиптической.

Авторы настоящей статьи поставили перед собой задачу проанализировать механизм плавного изменения форм гистерезиса и параметров, производных от него, в зависимости от вариации соотношения полуосей эллиптической траектории движения цапфы, установленной в опоре с кольцевым демпфером из материала МР [7].

Рассмотрим механизм возникновения гистерезиса в опоре с демпфером из материала МР (рисунок 1).

 

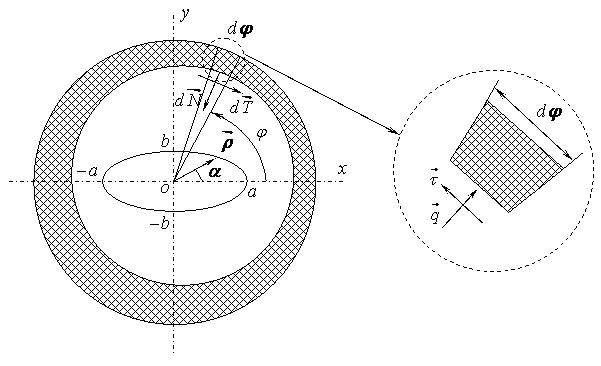
Рисунок 1 – Расчётная схема кольцевого демпфера

Закон движения центра цапфы зададим в параметрическом виде:

                                                                            

В выражении  и  - центр эллиптической траектории (постоянное смещение),  и  - величины горизонтальной и вертикальной полуосей эллипса,  - параметр, принимающий значения от 0 до .

Спроектировав вектор смещения  на нормаль и касательную произвольного бесконечно малого элемента, расположенного под углом  (рисунок 1), получим закон изменения во времени обжатия элемента демпфера  и касательного смещения цапфы относительно элемента .

                                            

В выражении  - величина натяга, с которым демпфер установлен в коаксиальное пространство между опорой и цапфой. Натяг определяется следующим выражением:

                                                                                  

где  - толщина демпфера до монтажа,  - радиус опоры,  - радиус цапфы.

Подставив в закон изменения вектора смещения во времени , и сгруппировав множители при  и , получим:

            

Из легко получить величины амплитуд обжатия  и касательных смещений цапфы относительно элементов демпфера , а также производных  и  по параметру , необходимые для вычисления реакций:

                                              

                          

                                                                

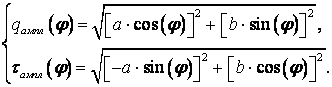
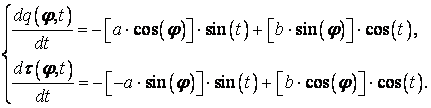
Положительному значению производной  соответствует ветвь нагружения на петле гистерезиса, возникающей в элементе демпфера вследствие внутреннего трения в материале МР, а отрицательному значению – ниспадающая ветвь разгрузки (рисунок 2). Аналогично при смене знака производной  с положительного на отрицательный возникает переход от нагружения к разгрузке на петле гистерезиса от граничного трения элемента демпфера о корпусные детали (рисунок 3).

В соответствии с формулой , параметры нагружения  и  при нагружении равны 1 и  – при разгрузке.

Для отыскания реакций по известным смещениям необходимо задаться законом, связывающим деформации и напряжения материала МР с учетом гистерезиса. Для этого воспользуемся моделью материала МР, предложенной Пономарёвым Ю.К. и дополненной корректировкой при малых амплитудах деформации, когда процессы нагружения и разгрузки не успевают влиться в граничный процесс:

                              

где  - текущая деформация,  - начальная деформация,  - амплитуда деформации,  - упругая линия материала,  - толщина петли гистерезиса,
 - остаточная деформация [5].

В рамках методики расчета принято допущение об отсутствии сдвиговых деформаций элементов демпфера. Для приближенного учёта сил трения, возникающих на границе материала МР и цапфы, применяется множитель , учитывающий эффект предварительных смещений.

          

где -  - коэффициент, задающий величину интегральной зоны предварительных смещений.

Теперь, зная распределение нормальных напряжений и коэффициентов трения, можно отыскать нормальные и тангенциальные реакции элементов демпфера, умножив напряжения на площади элементов.

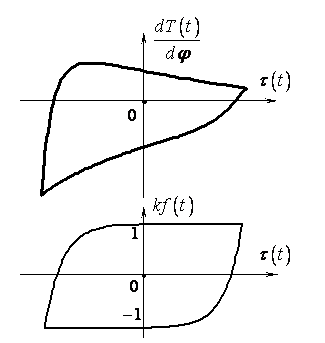
В результате вычисления по формулам - получаем петли гистерезиса в бесконечно малых элементах демпфера (рисунок 2,3).

Рисунок 2 – Типичный гистерезис в элементе демпфера вследствие внутреннего трения в материале МР	Рисунок 3 – Типичный гистерезис от граничного трения элемента демпфера о корпусные детали и соответствующий закон изменения множителя коэффициента трения

Спроектировав нормальную и касательную часть реакции элемента на оси координат,

                        

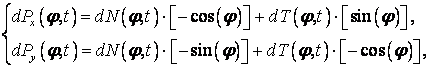
и проинтегрировав эти проекции по всей протяженности демпфера, получим полную реакцию демпфера.

                                                                        

Угловое положение  вектора смещения , угловое положение  вектора реакции  и сдвиг фаз между ними  можно найти следующим образом:

                                

                                         

                                                                                              

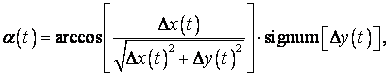
Так как реакция демпфера  и смещение центра цапфы  являются векторами, операция деления для которых не определена, жёсткость демпфера следует искать в комплексном виде. При этом действительная часть жёсткости соответствует упругой реакции демпфера, а мнимая часть – неупругой, отнесённых к модулю вектора смещения цапфы.

                                    

                                  .                                  

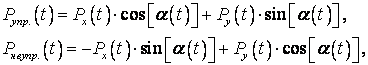
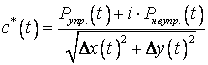Рассеянная энергия находится путём интегрирования произведений реакций  и   на соответствующие приращения  и  по параметру :

                                                                      

Момент сопротивления движению цапфы находится как сумма произведений сил  и   на соответствующие приращения смещения  и :

                                                  

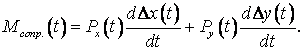
Суммарная рассеянная энергия за цикл нагружения:

                                                                

Потенциальную энергию упругой деформации и коэффициенты поглощения ищем в традиционном виде:

                                                                        

                                                                        

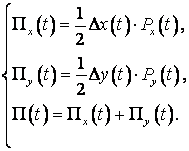
По описанному в статье алгоритму была составлена программа в интегрированном математическом пакете Mathcad и проведено широкое исследование упруго-гистерезисных характеристик и их производных (сдвига фаз, жёсткости, рассеянной и потенциальной энергии, коэффициентов поглощения).

На рисунке 4 представлены эпюры нормальных и касательных давлений

 

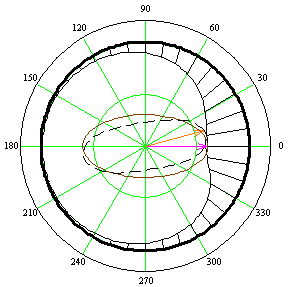
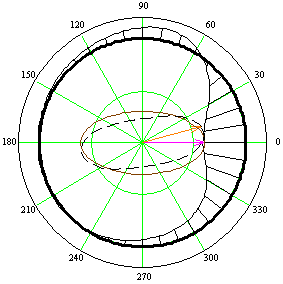
Рисунок 4 – Эпюры нормальных сил  и касательных сил  в демпфере

 

При вращении вектора силы относительно центра цапфы вектор перемещения отстает от вектора силы. При этом, вся эпюра давлений со стороны материала МР на цапфу вращается синхронно с вектором силы, качественно изменяясь в процессе движения вектора смещения.

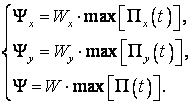
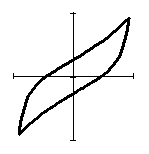
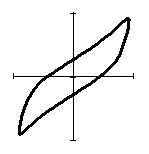
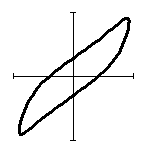
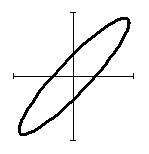
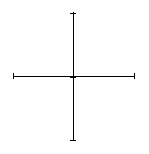
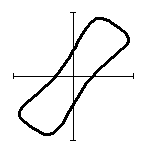
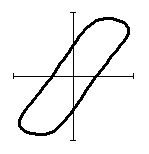
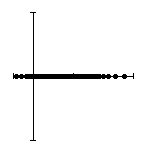
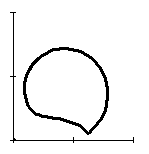
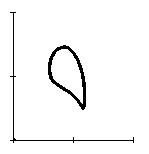
В таблице 1 представлены формы петель гистерезиса при различных соотношениях полуосей эллиптической траектории и соответствующие жёсткости , изображённые на комплексной плоскости.

Таблица 1 – трансформация гистерезиса в кольцевом демпфере.

Соотношение полуосей эллиптической траектории
0,00	0,25	0,50	1,00

 

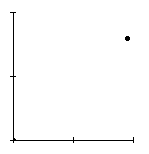
Из таблицы 1 видно, что при одноосном нагружении () петля гистерезиса в проекции на ось  представляется в традиционном виде с заострёнными концами при смене знака скорости деформации, а в проекции на ось  - в виде точки в начале координат. При постепенном увеличении коэффициента  от  до  форма траектории меняется от прямой линии до окружности, а гистерезис в проекциях на оси координат  и  трансформируется к эллипсу.

На рисунке 5 показаны графики, на которых по оси абсцисс отложены относительные амплитуды деформации , а по оси ординат –коэффициенты поглощения  для пяти различных соотношений полуосей эллиптической траектории .

Из рисунка 5 видно, что при движении цапфы по круговой траектории () коэффициент поглощения наибольший. При этом максимумы коэффициентов поглощения при различных соотношениях полуосей достигаются при одном и том же значении относительной амплитуды деформации .

Рисунок 5 – Влияние соотношения полуосей эллиптической траектории
на коэффициент поглощения демпфера

 

Литература

1.    Voigt W., Ann. d. Phys., vol. 47, p. 671, 1892.

2.    Pian T.H.H., Hallowell F.C., Structural Damping in a Simple Built-up Beam, Processing of the First U.S. Natural Congress of Applied Mechanics, ASME, p. 97-102, 1952.

3.    Goodman L.E., Klump J.H., Analysis of Slip Damping, Journ. Of Appl. Mech., N3, 1956.

4.    Я.Г. Пановко. Внутреннее трение при колебаниях упругих систем. Гос. изд-во ФМЛ -М., 1960.- 194 с.

5.    Чегодаев Д.Е., Пономарёв Ю.К. Демпфирование. – Самара: изд-во СГАУ, 1997.- 334 с.

6.    Ермаков А.И., Пономарёв Ю.К., Паровай Ф.В., Котов А.С. Новые средства виброзащиты в машиностроении на основе высокодемпфированного материала «МР». В сб. научн. тр. «Проблемы строительного и дорожного комплексов», вып. 4 – Брянск: БГИТА, 2006. – с. 16-19.

7.    Пономарёв Ю.К., Гунин В.А., Котов А.С. и др. «Расчёт характеристик упругодемпфирующих опор трубопроводов с применением материала МР (металлорезины)». В сб. трудов международного конгресса «Машиностроительные технологии» - МТ-04, Варна-София, Болгария, 2004, с. 128-131, изд-во Болгарской АН.