ОБЩАЯ И ИНЖЕНЕРНАЯ ПОСТАНОВКА ЗАДАЧИ ОПТИМИЗАЦИИ ПРОЦЕССА ВЗАИМОДЕЙСТВИЯ ЭЛЕМЕНТОВ СИСТЕМЫ «МЕСТНОСТЬ-МАШИНА»

 

Синицын С.С., Синицына Т.С.  (БГИТА, г. Брянск, РФРФ)

 

It is established, that for optimization of process of interaction of elements system «soil – machine» it is necessary to order private criteria by allocation of global criterion. 

 

Математическая постановка задачи оптимизации заключается в следующем [1]: задано множество  и функция  , определенная на ; требуется найти точки минимума или максимума функции    на . Задачи минимизации и максимизации функции   на  множестве  записываются в виде:

                                                            (1)

                                                                     (2)

При этом   называется целевой функцией,  - допустимым множеством, любой элемент  ( принадлежит  ) – допустимой точкой задачи (ее решением).

Решения задач (1), (2), т.е. точки минимума и максимума функции   на   называют также точками экстремума, а сами задачи –экстремальными. Причем при решении задач оптимизации чаще всего рассматриваются задачи минимизации.

В зависимости от вида целевой функции   оптимальное решение  может быть либо точкой локального минимума, либо точкой глобального минимума.

Вектор   называется точкой локального (относительного) минимума, если для всех точек  , принадлежащих - окрестности   этой точки, функция   не принимает меньшего значения:

          при всех                      (3)

Вектор   является точкой глобального (абсолютного) минимума, если ни в одной другой точке допустимой области  функция   не принимает меньшего значения:

              при всех                                  (4)

Таким образом, глобальный минимум – это наименьший из всех локальных минимумов. На рисунке 1 показаны точки локального  () и глобального () минимумов для произвольной кривой целевой функции   [2].

Различают необходимые и достаточные условия оптимальности. Для того чтобы точка   являлась оптимальным решением (локальным минимумом), необходимо и достаточно, чтобы в этой точке первая производная минимизируемой функции равнялась нулю, а ее вторая производная была положительной величиной:

 

                                            (5)

 

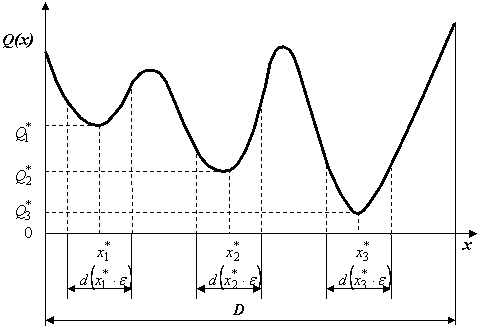
Рисунок 1 – Произвольная кривая с двумя локальными и одним глобальным  минимумами

 

Для решения задачи оптимизации тягово-сцепных свойств  колесных транспортно - технологических машин необходимо установить границы подлежащей оптимизации системы, определить количественные критерии, на основе которых можно произвести анализ вариантов с целью выявления «наилучшего», осуществить выбор внутрисистемных переменных параметров, независимым вариантом которых можно достичь «наилучшего» варианта функционирования системы.

В решении вопроса выбора границ объекта оптимизации в первом приближении можно ограничиться системой «движитель – трансмиссия», поскольку это достаточно автономная система, имеющая все исходные признаки для возможной оптимизации, а именно: внешние  факторы, обозначаемые вектором    внутренние конструктивно-технологические параметры     выходные параметры     

Управляемые внутренние параметры   и выходные характеристики  определяют свойства системы как объекта оптимизации, а внешние факторы  образуют среду, в которой функционирует система.

Такое формализованное представление системы «движитель – трансмиссия» позволяет рассматривать ее как «черный ящик»,  к управляющему органу которого приложены возмущающие  и управляемые   воздействия, формирующие численные значения выходных характеристик  

В этом случае решение задачи оптимизации тягово-сцепных свойств  сводится к параметрической оптимизации, заключающейся в выборе управляемых параметров  , принадлежащих допустимой области  и обеспечивающих экстремальное значение критерия оптимальности   

Поскольку тягово-сцепные свойства объединяют комплекс оценочных показателей, то стремление обеспечить оптимальность всей их совокупности приведет к многокритериальной оптимизации, что затруднит практическую реализацию этого мероприятия. Поэтому следует упорядочить частные критерии оптимальности по их важности путем выделения обобщенного глобального критерия оптимальности. Такая постановка задачи оптимизации обуславливает необходимость четкого функционального разделения свойств физической системы «опорная поверхность – движитель – трансмиссия» на факторы среды  , управляемые параметры   и характеристики   , а также выделение из них только наиболее существенных с целью последующего использования их при построении математической модели «системы».

Литература

1. Сухарев А.Г. Курс методов оптимизации./ А.Г. Сухарев. – М.: Наука, 1986.- 280 с.

2. Батищев Д.И. Методы оптимального проектирования./ Д.И.Батищев – М.: Радио и связь, 1984. -255 с.