ИСПОЛЬЗОВАНИЕ ВОЛНОВОЙ ТЕОРИИ ДЕФОРМАЦИИ ПРИ ОПИСАНИИ ВЗАИМОДЕЙСТВИЯ ГУСЕНИЧНЫХ ЛЕСНЫХ МАШИН СО СЛАБЫМИ ГРУНТАМИ
Лобанов В.Н. (БГИТА, г. Брянск, РФ)
Formulae for determining soil consistency and speed of its particles traverse between engine and wave front taking into account the time of process passing are obtained.
В процессе работы колебания корпуса лесных машин, возникающие при их движении по неровной поверхности лесосеки, вызывают дополнительное увеличение давления гусеницы на почву и приводит к изменению поля напряжений в толще грунта. При этом переуплотнение почво-грунта происходит не только в верхних слоях, но и на глубине.
Определение основного параметра механики грунтов – нормального напряжения сжатия представляет собой сложную задачу, особенно для случаев динамического нагружения, которые характеризуются незначительным временем воздействия.
Процессы взаимодействия гусеничных машин со слабыми лесными грунтами описываются без учета изменения их физико-механических свойств при деформировании и без учета времени протекания процесса.
Цель нашей работы - определить плотность и скорость деформации почвы при динамическом нагружении с использованием положений волновой теории деформации.
В случае одномерных движений с цилиндрическими и плоскими волнами основными искомыми функциями являются в общем случае компоненты тензора напряжения, плотность или объемная деформация грунта и скорость частиц, а определяющими параметрами – константы, входящие в уравнения движения и в граничные и начальные условия задачи. Координатную ось Z выбираем совпадающей с направлением движения частиц грунта (см. рисунок).
Основные уравнения, описывающие вертикальное движение частиц грунта в переменных Эйлера, имеют вид [1, 3]:
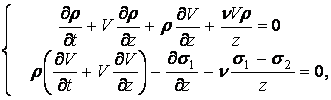(1)
где ν - коэффициент, зависящий от формы движителя (для плоской - ν = 0, для цилиндрической - ν = 1, для сферической - ν = 2); ρ(z,t) - плотность грунта; V(z,t) - скорость перемещения частиц грунта.
Рисунок
При движении лесных гусеничных машин по лесосеке грунт под движителем изменяет свою форму и объем. В толще грунта под движителем возникает волна деформации [3], под действием которой частицы грунта перемещаются вниз вдоль оси z.
В соответствии с законом сохранения массы изменение массы грунта, содержащейся в объеме, охваченном действием волны, равно разности потоков массы грунта, входящего через площадку S перпендикулярную координатной оси (в данном случае z) и выходящего через параллельную ей грань.
Уравнение непрерывности для данного случая записывается в виде [2]:
∆ρ·u = ρ2 ·V2 - ρ1 ·V1, (2)
где ∆ρ = ρ2 - ρ1; ρ1 - плотность грунта сзади фронта волны; ρ2 - плотность грунта перед фронтом волны; u - скорость волны; v1 и v 2- соответственно скорости частиц грунта после и перед фронтом волны.
Изменение напряжения в выделенном объеме грунта под действием волны описывается следующим уравнением (см. рисунок):
[( ρ ·V)2 - (ρ ·V)1]u = σ2 + (ρ ·V2)2 – σ1 – (ρ ·V2)1, (3)
где σ1 и σ2- соответственно напряжения, возникающие в грунте сзади и перед фронтом волны.
Так как перед фронтом волны находится невозмущенная среда, то она характеризуется следующими параметрами
ρ2 = ρ0; V2 = 0; σ2 = 0.
Поэтому уравнения (1) и (2), сведенные в систему (3), принимают вид:
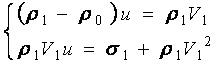. (4)
Решаем полученную систему уравнений относительно ρ1, подставив значение u из первого уравнения во второе:
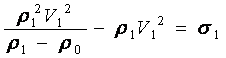(5).
В окончательном виде после преобразований уравнения (5) получим выражение для определения плотности грунта ρ1 в его толще после прохода машины, т.е. плотность грунта между движителем и фронтом волны
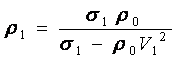(6)
Напряжение в толще грунта между движителем и фронтом волны σ1 определяем по уравнению [3]:
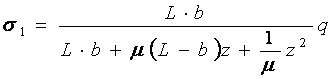, (7)
где L и b- соответственно опорная длина и ширина гусеницы, м; q-давление гусеницы на поверхность грунта, Н/м2; z-глубина, на которую распространяется фронт волны (в расчетах z = 2b), м; μ-коэффициент Пуассона для грунтов.
В общем случае скорость V1 перемещения частиц грунта за фронтом волны зависит от относительной деформации грунта. Для определения скорости V1 рассмотрим уравнения системы (1), которые описывают поведение грунта, расположенного между движителем, движущимся со скоростью V0, и фронтом волны [4].
Так как относительная деформация грунта изменяется в пределах от 0 до 1, то его плотность в пространстве между гусеничным движителем и волной можно считать практически постоянной. Тогда первое уравнение системы (1) примет вид
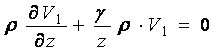
или с учетом, что ρ ≠ 0
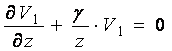(8)
Решая уравнение (8) с граничным условием
V0 =V1 (z= V0 t, t) при t ≥ 0, (9)
найдем скорость V1 (z, t). Решение будем искать в виде:
V1 (z, t) = V1 ( t) · V1 (z), где V1 (t) ≠ 0. (10)
Подставляя (10) в (8) и разрешив его относительно функции V1(z), получим уравнение
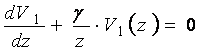или 
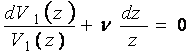(11)
Из (9) видно, V1(z, t) убывающая по z
функция, так как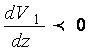 
.
Интегрируя уравнение (11), имеем
или 
, (12)
где с - производная постоянная.
Подставляя выражение V1(z) в уравнение (10), получим
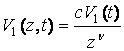. (13)
Используя граничное уравнение (9) z = V0 t, имеем выражение для V0
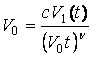, при t ≥
0. (14)
Решаем совместно уравнения (14) и (13), получим
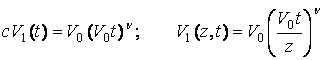. (15)
В окончательном виде получаем выражение для определения скорости движения частиц грунта V1:
.
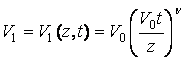(16)
Полученные зависимости (6), (7) и (16) позволяют определить поле напряжений σ1, плотность грунта ρ1 и скорость перемещения частиц грунта V1 между движителем и фронтом волны, возникающей при динамическом воздействии звеньев гусениц движущейся машины.
Литература
1. Баладинский, В.Л. Динамика разрушения сред в строительстве и горном деле [Текст] / В.Л.Баладинский, В.Г.Моисеенко, А.В.Фомин. // Оптимальное взаимодействие: симпозиум по террамеханике. - Суздаль, 1992. -С 251-258.
2. Лобанов, В.Н. Исследование взаимодействия гусеничного движителя с деформируемым грунтом [Текст] / В.Н. Лобанов. // Оптимальное взаимодействие: симпозиум по террамеханике. - Суздаль, 1992. -С 93-97.
3. Ляхов, Г.М. Волны в грунтах и пористых средах. [Текст] / Г.М. Ляхов– М.: Наука, 1982. – 286 с.
4. Умов, Н.А. Избранные сочинения. [Текст] / Н.А.Умов – М.: Наука, 1950. – 412 с.