ПОВЫШЕНИЕ ЭКОЛОГИЧЕСКИХ СВОЙСТВ КОЛЕСНЫХ ТРАНСПОРТНО-ТЕХНОЛОГИЧЕСКИХ МАШИН

 

Синицын С.С., Синицына Т.С.  (БГИТА, г. Брянск, РФРФ)

 

The criteria of optimum capacity controlled parameters and target junctions have been substantiated. The parametric optimization of traction coupling properties to the criterion or minimum energy consumption has been made.

 

Строительство транспортных магистралей, разработка полезных ископаемых, механизация лесной промышленности и сельского хозяйства требует создания и выпуска внедорожных колесных транспортно-технологических машин с высокими экологическими характеристиками. Комплексной оценкой экологического совершенства колесного движи­теля являются потери энергии в контакте пневматических колес с опорной поверхностью.

Известно, что на сопротивление качению пневматического колеса существенное влияние оказывает давление воздуха в шине. А поскольку этот параметр является единст­венным в системе "движитель - опорная поверхность", который можно оперативно изме­нять в процессе эксплуатации, то представляется перспективной задача определения вели­чин давления воздуха, обеспечивающих минимальные потери энергии при работе колес­ных машин в различных эксплуатационных условиях, а, значит, и высокие экологические характеристики.

Применяя расчетную схему, в которой колесо отождествлено с эллипсоидом [1], определим составляющую сопротивления качению из-за колееобразования как сумму го­ризонтальных реакций грунта на криволинейную ω поверхность контакта шины с опор­ной поверхностью, а именно:

                                             (1)

где ω - сопротивление грунта смятию элементарной площадкой поверхности шины;

       а - угол между вектором σ и осью z.

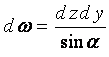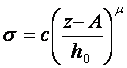Так как    , а   , то

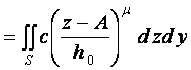,                              ( 2)

где с, μ -  параметры грунта; h₀- базовая деформация грунта; z - текущая ордината точек поверхности контакта;  А - расстояние от оси колеса до поверхности грунта; S - горизонтальная проекция поверхности.

Разложив  (z - А)^μ  в  степенной ряд и определив пределы интегрирования (R – - h_Г -  h_ш  - ≤  z  ≤ R- h_ш) и (0 < у ≤ b – bz² /2R²) получим для первого члена ряда:

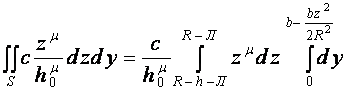 .                 (3)

После интегрирования и преобразования имеем:

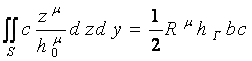,                          (4)

С учетом оставшихся членов ряда окончательно получим:

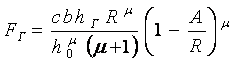 .                          (5)

Допуская, что  при малых деформациях шин  , имеем:

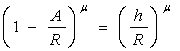, тогда

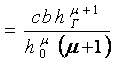,                                              (6)

где b- полуось условного эллипсоида.

Для определения составляющей сопротивления качению колеса, обусловленную потерями энергии на гистерезис в шине, воспользуемся известной зависимостью  [2]

,                                     (7)

где В_п - ширина протектора; h_щ - радиальная деформация шины; k_ш - коэффициент, характеризующий внутренние потери энергии в шине.

Уравнение для определения радиальной деформации шины получаем из условия равенства реакций грунта в плоской зоне контакта нормальной нагрузке на эту зону со стороны колеса, то есть:

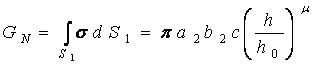,                       (8)

где  - полуоси эллипса, отображающего форму плоской                           зоны контакта; -  часть нормальной нагрузки со стороны колеса, воспринимаемая плоской зоной контакта.

Поскольку  ,  , то 

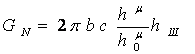, а значит 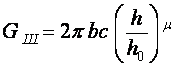.            (9)

С другой стороны

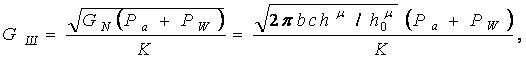        (10)

где Р_а - атмосферное давление; Р_W - избыточное давление воздуха в шине;

       К  - эмпирический коэффициент, зависящий от   конструкции шины.

Приравняв правые части  выражений  (9)   и (10)   и решив относительно , получим

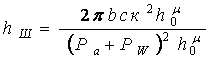.                                        (11)

Таким образом, с учетом того, что 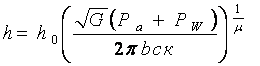 [1] зависимость для определения сопротивления качению ведомого пневматического колеса принимает следующий вид:

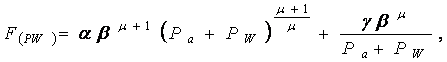     (12)

где  

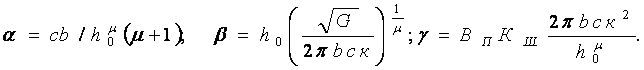
Для решения задачи отыскания минимально возможного сопротивления качению прибегаем к монопараметрической оптимизации целевой функции (12), заключающейся в ее оптимизации. Тогда формализованная задача  отыскания оптимальных значений давлений , доставляющих минимум функции  , принимает  следующий вид:

,

,                                      (13)

где   Р_min, Р_max - минимальное и максимальное давление воздуха в пневматической шине.

Выражая  частную производную от функции    через частный дифференциал, имеем

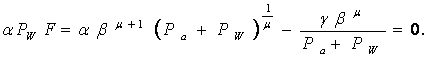            (14)

Решив уравнение  (14) относительно  Р_W, окончательно получим:

или

    (15)

Экспериментальная проверка полученной зависимости показала достаточно близ­кое совпадение расчетных и опытных данных. Так, например, при исследованиях шин 530-610Р (b = 0,4м; В_п = 0,5м; К_п= 1,6×10 ^{- 4}Па; к = 0,95×10 ^-5 МПа/Н⁰⁵; G = 16000 Н) на забо­лоченной луговине (μ = 0,5; с = 1,5×10⁵ Па) установлено, что минимальное сопротивление качению обеспечивается при   =0,1 МПа. Расчетное же значение  составляет 0,108 МПа.

Таким образом, проведенные исследования позволяют рекомендовать зависимость (15) для практического применения при решении задачи минимизации энергозатрат на пе­редвижение колесных машин по деформируемому основанию.

В эксплуатационных условиях реализация этого мероприятия вполне осуществима за счет более эффективного использования дистанционных систем регулирования давле­ния воздуха в шинах, которыми оснащены колесные машины высокой проходимости. Од­нако, с учетом того, что колесные машины эксплуатируются на самых разнообразных опорных поверхностях, начиная с дорог общего пользования с асфальтобетонным покры­тием и кончая заболоченными лесными почво-грунтами, то более перспективным направ­лением следует считать автоматизацию процесса минимизации сопротивления качению за счет применения экстремальных систем регулирования давления, обеспечивающих авто­матический поиск и поддержание оптимальных величин давления воздуха в шинах.

Литература

1. Лазарев В.В., Синицын С.С. Анализ процесса колееобразования при качении пневматического колеса по деформируемому грунту// Известия ВУЗов. Машиностроение. Вып. 5. - М.: МВТУ им. Н.Э. Баумана, 1983.

2. Агейкин Я.С. Вездеходные колесные и комбинированные движители. - М.: Ма­шиностроение, 1972.

3. Лазарев В.В., Синицын С.С. Определение глубины колеи и радиальной деформа­ции пневматического колеса при качении по грунту// Лесосечные, лесоскладские работы и сухопутный транспорт леса. -Вып. 11. Межвуз. сб. науч. тр. -Л.: ЛТА, 1982.