АНАЛИТИЧЕСКАЯ ОЦЕНКА МАШИННОЙ ДЕГРАДАЦИИ ПОЧВЫ

 

Синицын С.С., Синицына Т.С.  (БГИТА, г. Брянск, РФ РФ)

 

The analytical relation for definition of pressure of a propulsor on a soil is designed. Contains minimum quantity of trial-and-error parameters.

 

Расчетные методы определения давления колес на почву базируются на значительном числе эмпирических и полуэмпирических зависимостей. В то же время есть попытки использовать для этих целей и аналитические зависимости, полученные при использовании различных моделей почвы и колеса. Однако препятствием для вычисления максимального давления по этим формулам служит недостаточность информации по параметрам моделей колеса и почвы. Поэтому проведем исследования с целью получения аналитической зависимости, содержащей минимальное количество легко определяемых  коэффициентов.

Воспользуемся для этого известной степенной зависимостью, представленной в следующем виде 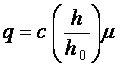[1]:

                                              ,                                              (1)

где   - размерный коэффициент;  = 0,01 м.

Как следует из этого уравнения,  для определения величины давления колеса на почву необходимо знать значение глубины колеи  h.

Условие равновесия вертикальных сил, действующих в пятне контакта можно представить в следующем виде 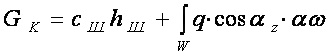[2]:

,                          (2)

где    - нормальная нагрузка, действующая на колесо;  - радиальная жесткость шины; w - площадь криволинейной части контакта;  - угол, образованный направлением действия силы  q с осью  z.

Так как между элементарной площадкой на профиле шины и ее проекцией на плоскость   существует зависимость

,

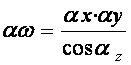а уравнение (1) можно представить следующим образом:

,

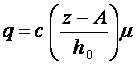то уравнение (2) принимает следующий вид:

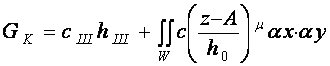                       (3)

Используя для  z его значение из характеристического уравнения эллипса, после интегрирования  и  ряда преобразований,   для криволинейной зоны контакта получаем

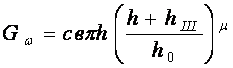                                      .                            (4)

Для плоской зоны контакта имеем

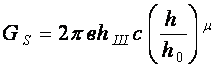                                   ,                                   (5)

где  - площадь плоской зоны контакта.

Поскольку , то

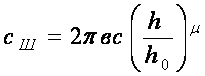                                  ,                                (6)

но с другой стороны

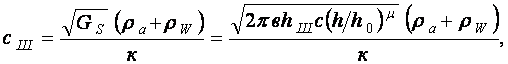                                       (7)

где   - атмосферное давление, Па;  - давление в шине, Па;  к  - параметр шины, Н^1/2/ м.

Приравняв правые части уравнений для   и решив относительно   , получим

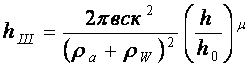                                    .                         (8)

Тогда уравнение (3) после соответствующих преобразований принимает следующий вид:

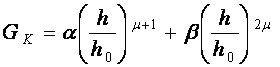,                               (9)

где  ;      .

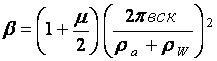Решив уравнение (9)  относительно  , получаем:

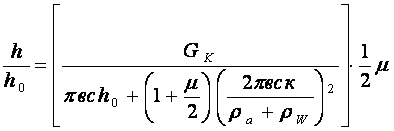.                 (10)

Ввиду  малости первого слагаемого в знаменателе уравнения  (10) оно может не учитываться, тогда после преобразований получим

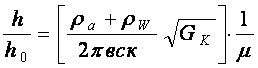.                                 (11)

С учетом зависимости  (11) уравнение (1) для определения максимального давления колеса на почву принимает следующий вид:

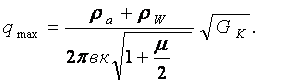                                                           (12)

Полученное уравнение отличается простотой структуры, наглядностью степени влияния каждого параметра, и содержит лишь только два эмпирических коэффициента: к - для шины   и m  - для грунта. Определение этих коэффициентов не составляет труда.

Литература

1. Вялов С.С. Реологические основы механики грунтов. – М.: Стройиздат, 1979.- 436 с.

2. Синицын С.С. Математическая модель колеса с эластичной шиной // Эксплуатация лесовозного подвижного состава : Межвуз. сб. науч. трудов. - Свердловск, 1987.