ИССЛЕДОВАНИЕ ПЛАВУЧЕСТИ МЕТАЛЛИЧЕСКОГО БАЛЛОНА, ИСПОЛЬЗУЕМОГО НА СПЛОТКЕ ЛЕСОМАТЕРИАЛОВ  С ОГРАНИЧЕННОЙ  ПЛАВУЧЕСТЬЮ

 

Патякин В.И., Огар П.М., Угрюмова  С.Н.

(ГОУ ВПО «БрГУ», г. Братск, РФ)

 

       As a result of research of buoyancy of the metal cylinder used during a coupler of log and log products, the schedule of dependence of pushing out force from depth of immersing is received.

 

Произведем исследование плавучести баллона в свободном состоянии    (без   нагрузки).   Баллон   представляет   собой   металлическую   трубу   с металлическими заглушками.

По закону Архимеда, чтобы тело находилось на плаву, требуется соблюсти условие, где выталкивающая сила (А) будет больше или равна силе тяжести.

                                                  ;                                                      (1)

Сила тяжести вычисляется по формуле:

                                         ;                                       (2)

где  - масса воздуха находящегося в баллоне, кг.

 - масса баллона, кг.

g - ускорение свободного падения, м/с².

Масса баллона равна сумме масс трубы и стальных заглушек по торцам трубы:

                                               ;                                               (3)

Выталкивающая   сила по  закону  Архимеда  равна  произведению плотности жидкости ( - вода, 1000 кг/м³), объема тела погруженного в жидкость (V_Т) и ускорения сводного падения:

                                            ;                                                (4)                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                   

Зададимся необходимыми параметрами для вычисления:

D = 0,8м - диаметр трубы;  L = 4,0м - длина трубы;

S = 0,008м - толщина стенки трубы;

D_загл = 0,8м   диметр заглушек;

l_загл = 0,008м - длина заглушек.

Материал баллона Ст3...20. (р_ст - 7850 кг/м³)

Для начала произведем расчет плавучести баллона при условии , когда тело находится под поверхностью воды.

;                                         (5)

                                                      ;

где

, м³ ,

где r -внутренний радиус трубы, м

                                               , кг;                                         (6)

, кг;

;

где , ,

- наружный радиус трубы, м

 - радиус заглушки, м

;

Эту зависимость можно представить:

;

Соответственно получим:

 кг;

Путем математических расчетов выводим    

;

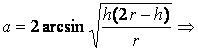
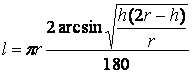Используя формулу и заменяя в ней  на произведение F и L получаем:                                                                                                                                                                                                                                                

;

После некоторых преобразований, получаем:

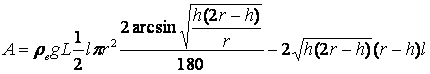 ;    (7)

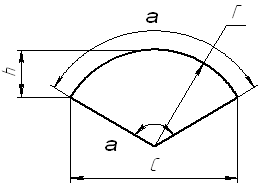
Данная формула верна при условии погружении баллона на глубину   (рис. 1), при h > r необходимо ввести угловую поправку (360- ).

При этом формула принимает вид:

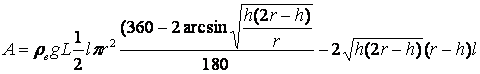 ;     (8)

Подставляя различные величины  h (от 0 до 0,8 м) в формулы построим график зависимости выталкивающей силы А от глубины погружения h.

Сила тяжести баллона равна:

;

;

где .

Данная величина является критической, т.к. при данных расчетах баллон находится в состоянии полного погружения под поверхность воды.

Произведем расчеты и построим график зависимости выталкивающей силы от глубины погружения баллона.

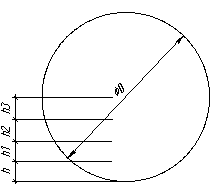
Разобьем окружность на 20 сегментов на расстоянии 0,02м. (рис. 1)

Рисунок 1

 

;

где F - площадь сегмента, м²;

       r - радиус сегмента, м;

       l - длина дуги, м;

       h - высота сегмента (глубина погружения), м.

;

, где  - центральный угол в градусах,

 

Таблица 1 - Данные для построения графика

h, м	0	0.04	0.08
А,Н	0.00	368.33	1025.48
h, м	0.12	0.16	0.2
А,Н	1853.37	2805.44	3852.17
h, м	0.24	0.28	0.32
А,Н	4971.65	6146.07	7360.06
h, м	0.36	0.4	0.44
А,Н	8599.73	9852.03	11104.34
h, м	0.48	0.52	0.56
А,Н	12344.01	13558.00	14732.42
h, м	0.6	0.64	0.68
А,Н	15851.90	16898.63	17850.70
h, м	0.72	0.76	0.8
А,Н	18678.59	19335.74	19704.07

 

График зависимости выталкивающей силы от глубины погружения

 

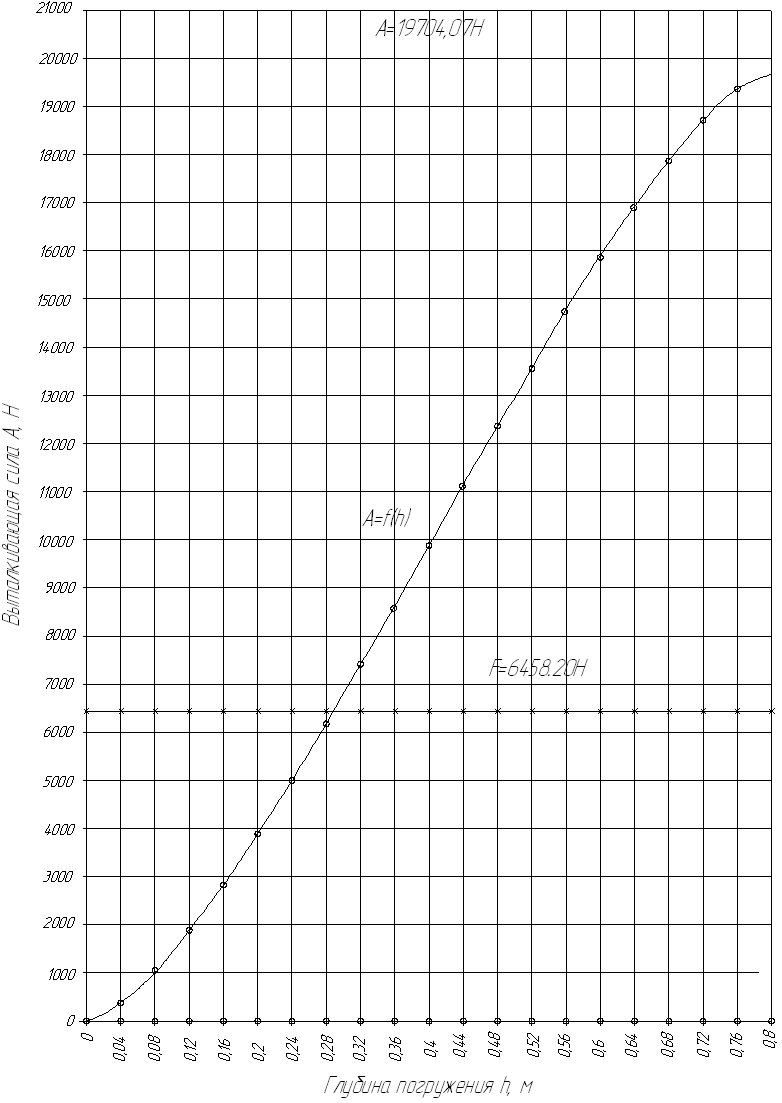
      В ходе теоретических исследований  по определению плавучести  металлического баллона, используемого в процессе сплотки лесоматериалов  с ограниченной плавучестью, получен график зависимости выталкивающей силы от глубины погружения пучка с ограниченной плавучестью.