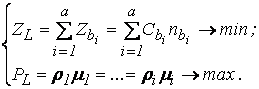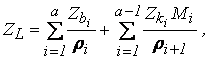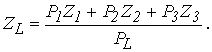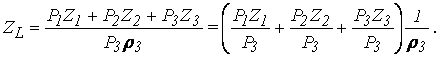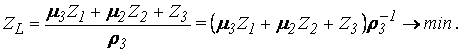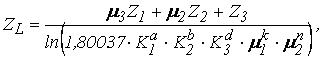ФОРМАЛИЗАЦИЯ КРИТЕРИЯ ОПТИМИЗАЦИИ СИСТЕМ МАШИН СТОХАСТИЧЕСКИМИ ИНТЕРВАЛАМИ ОБРАБОТКИ ЗАГОТОВОК

 

Иванишин Т.В. (НЛТУУ, г. Львов, Украина)

 

Mathematical models of target-oriented function have been synthesized for the structure of synchronic multimachine production systems with constant operation rhythm for machining of windows and doors blanks estimation and optimizing.

 

Актуальность проблемы. Положения о необходимости создания математических моделей, которые бы непосредственно отображали взаимосвязь технических и экономических показателей работы технологического оборудования, были сформулирована ещё в теории производительности линий [1]. Такие аналитические зависимости должны определяют влияние любых изменений качественных параметров анализируемых вариантов построения многостаночных систем на их экономические показатели и быть пригодными для проведения структурно-параметрической оптимизации линий за выбранным критерием эффективности их функционирования. А с учётом того, что работа деревообрабатывающих станков постоянно подвергается возмущающему влиянию большого количества стохастических факторов, то синтез адекватных оптимизационных моделей процесса обработки заготовок существенно  усложняется [2,4].

Постановка задачи. С переходом деревообрабатывающей отрасли из массового производства продукции на серийное, методика оценки работы машинной системы по критерию роста еë производительности постепенно отошла на задний план. Сегодня более актуальными являются экономические критерии оптимизации технологических процессов: величина приведенных инвестиций, эффективность капиталовложений, текущие затраты на единицу продукции, затраты производства и т.п.

Анализируя эффективность вариантов капитальных вложений или себестоимость выпуска продукции, чаще всего приходится решать статическую задачу выбора оптимальной структуры производственной многостаночной системы за среднегодовыми показателями еë функционирования (например, за критерием минимума суммарных приведенных затрат на выпуск продукции), без учёта фактора времени и связанных с ним изменений (дисконтирование доходов и затрат) [3]. Здесь нельзя ограничиваться только одной выбранной целевой функцией, так как без учета фактической производительности систем машин невозможно прогнозировать объëм производственной программы выпуска продукции. В этом случае целесообразнее применять метод двухкритериального определения оптимального варианта структуры линии: когда  затраты производства будут минимальными – Z_L ® min и одновременно приоритетными, а производительность машинной системы, по возможности, максимальной ­ – Р_L ® max. В таком случае структура многостаночной производственной системы будет оптимальной, когда выполняются условия:

 

(2)

 

где      Z_bі – затраты обработки заготовок на і-ом станке в линии;

       n_bі – число обработанных заготовок на і-ой операции;

      С_bі – себестоимость обработки единицы продукции на і-ом станке;

       а – количество машин в линии;

      r_і – коэфициенты использования станков в линии;

      m_і – цикловая производительность машин.

 

Методика решения задачи. Учитывая структуру системы уравнений (2) выбранной целевой функции, построим  математические модели оценки эффективности работы трëхстаночных систем машин с жесткой межагрегатной связью в условиях стохастической неопределенности варьирования параметров оборудования.  Расчет суммарных приведенных затрат производства единицы продукции для произвольной многостаночной системы можно вести по обобщённой математической модели на основании критерия минимума приведенных затрат [2]:

 

(3)

 

где      – затраты по межстаночных накопителях;

М_і – вместительность межстаночных буферных устройств.

 

На основании модели (3) для синхронной трëхстаночной линии с жëстким агрегатированием машин из номинальными производительностями Р₁, Р₂ и Р₃ (где на каждой операции себестоимость обработки одной заготовки составляет Z₁, Z₂ и Z₃) текущие затраты по агрегатах равны, соответственно, Z_b1 = Р₁Z₁, Z_b2  = Р₂Z₂ и Z_b3  = Р₃Z₃. Поскольку фактическая производительность линии, агрегатированная последовательно работающими станками, определяется фактической производительностью еë произвольной машины в потоке: Р_Л = Р₁r₁ = Р₂r₂ = Р₃r₃, то суммарные приведенные затраты на единицу продукции можно определить по формуле (М₂ = М₃ = 0):

 

(4)

Заменив фактическую производительность линии Р_L произведением качественных параметров Р₃ и r₃ третьего станка (4), который является определяющим в её структуре (окончание обработки заготовки свидетельствует об еë выходе с линии), получим

(5)

 

Отсюда, математическая модель целевой функции по критерию минимума приведенных затрат на единицу продукции обработки заготовок на трëхстаночной линии с индивидуальным ритмом работы и жëстким агрегатированием станков примет вид:

(6)

где       – соотношение цикловых производительностей первой и третьей машин в линии;  

 – соотношение цикловых производительностей второй и третьей машин в линии.

Достоверность расчётов целевой функции Z_L повысится, если аналитическую зависимость (6) объединить из синтезированным эмперическим уравнением [4], где коэффициент использования рабочего времени третьей машины r₃ определяется с учётом параметров Ерланга К_і оборудования, характеризующих случайность обработки заготовок на технологических операциях: , где  – дисперсия среднего значения продолжительности операции. Тогда получим следущую математическая модель:

(7)

где       – отношение цикловых производительностей первого и второго станков в линии;

                    

                    

 

        Эффективность функционирования многостаночных линий по критерию минимума приведенных затрат на обработку заготовок можно косвенно оценивать наложенными потерями рабочего времени оборудования, величина которых зависит от производительности станков Р_і и их местонахождения в структуре линии. Для синтеза такой математической модели (8) использована методика аппроксимации в регрессионную зависимость статистического массива значений приведенных затрат Z_Л механической обработки заготовок,  полученного во время имитационного моделирования на ЭВМ работы рассмотренных линий. На указанные случайные входные факторы К_і и m_j накладывались ограничения, установленные в процессе проведения производственного эксперимента: 1£ К₁ ¹ К₂ ¹ К₂ £ 60, 0,5 £ m₁ £ 2 и 0,5 £ m₂ £ 2.

(8)

        где     

   

   

   

   

Для реализации математической модели (8) смоделировано на ЭВМ более 16200 возможных вероятностных состояний трëхстаночной производственной системы с обработкой 500000 заготовок.

Выводы: Синтезированные математические модели целевой функции по критерию минимума приведенных затрат Z_L на обработку заготовок можно использовать на начальном этапе проектирования рациональных структур трëхстаночных систем с жëстким агрегатированием оборудования. Они пригодны для оценки эффективности работы и структурно-параметрической оптимизации уже скомпонованных и реально работающих на производстве линий с учетом характерных детерминированных и стохастических параметров оборудования.

 

Литература

1. Шаумян Г. А. Комлексная автоматизация производственных процессов. - М.: Машиностроение. 1973. - 639 с.

2. Дудюк Д. Л. Елементи теорії автоматичних ліній.- К.: 1998.- 192 с.

3. А.Г. Загородній, Ю.І. Стадницький. Менеджмент реальних інвестицій. - К.: Знання, 2000. - 209 с.

4. Иванишин Т. В. Идентификация процесса работы многостаночных производственных систем механической обработки брусковых заготовок оконных и дверных блоков// Актуальные проблемы лесного комплекса. Сборник научных трудов по итогам 5-ой международной научно-технической конференции “Лес-2004”. – Брянск: БГИТА, 2004, вып. № 8. – С. 227-230.