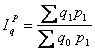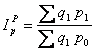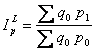АГРЕГАТНОЕ ОТНОШЕНИЕ КАК ВНУТРЕННЯЯ СТРУКТУРНАЯ ХАРАКТЕРИСТИКА ИНДЕКСНЫХ СИСТЕМ

 

Курицын А.В. (Филиал «РГЭУ “РИНХ”», г. Георгиевск, РФ)

Сологубов С.В. (ГТИ (филиал) СевКав ГТУ, г. Георгиевск, РФ)

 

Aggregate relation as inner structural character of index system. It has clear economical meaning. Its application in analytical purpose gives new stimulus for development of index theory.

 

В мировой и отечественной практике наиболее широко применяются объемные и ценовые индексы Пааше и Ласпейреса:

Индексы	Объема	Цены
Пааше
Ласпейреса

Перекрестным перемножением индексов Пааше и Ласпейреса получаются две индексные системы общего индекса:

                                                  (1)

и

                                                         (2)

Вопрос о практическом предпочтении (1) или (2) расчетной формулы до сих пор остается открытым. Исследователям предоставляется право, в зависимости от целей исследования, применять одну из двух формул расчета общего индекса, что не отвечает принципу универсальности при решении возникающих задач.

По мнению авторов, проблема кроется в отсутствии универсальной структурной характеристики, удовлетворяющей любой из индексных систем.

В настоящее время в качестве такой обобщающей характеристики выступает показатель индекса ковариации (I_COV), учитывающий одновременное изменении двух факторов. Впервые формулу индекса ковариации вывел В.И. Борткевич. В различных источниках данная формула встречается в виде:

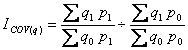                                       (3)

или

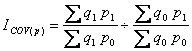                                       (4)

где - индекс ковариации по объему; - индекс ковариации по цене.

С помощью I_COV  общий индекс может быть представлен как:

I_p^P                                 I_p^L

 

                                   (5)

 

I_q^P                        I_q^L

Из этого следует, что группируя I_COV тем или иным способом с индексом цены или индексом объема, мы вынуждены относить совместное влияние двух факторов к одному из них. Тем самым мы либо увеличиваем, либо уменьшаем его реальное влияние на уровень I_W, в свою очередь, уменьшая или увеличивая влияние другого фактора. При этом происходит смена системы координат, так как механизм действия I_COV  таков, что одна система изменяет свое состояние (I_p^L × COV_p = I_p^P и I_q^L × COV_q = I_q^P) за счет изменения другой, усложняя проблему выбора формулы общего индекса. В этом авторы видят существенный методологический недостаток I_COV.

Если с использованием индексов объемной и ценовой ковариации представить переход от формулы (1) индексной системы к формуле (2) в виде ориентированного графа (см. рисунок 1), то можно увидеть, что индексы ковариации занимают место во внешнем контуре графа и, следовательно, отражают «внешнее» различие между двумя системами агрегатных индексов.

COVp

                                        ×                                   =

 

 

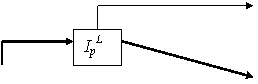
Iw

AR

Iw

                                        ×                          =

 

            =       ×                 :                                    =                 ×       =

IqL

IqP

                                                                            

 

COVq

                              :                                             =

                                       

 

Рисунок 1 – Ориентированный граф перехода от одной индексной системы к другой

 

В тоже время индексы Пааше, как и индексы Ласпейреса, имеют собственную («внутреннюю») структуру, которая, по сути, формирует их количественный уровень. Для оценки «внутренней» структуры индексов Пааше и Ласпейреса авторы предлагают использовать ещё один структурный показатель, который получается путем деления индексов объема на индексы цен.

Назовем этот показатель агрегатным отношением (AR) индексных систем (от английского – aggregate relation). Это показатель имеет следующее выражение:

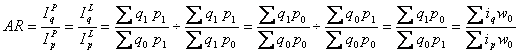  (5)

Как видно из рисунка 1, AR лежит внутри графа и, по мнению авторов, имеет конкретный экономический смысл, а именно:

1) AR – это отношение средневзвешенного индивидуального индекса объема (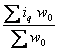) к средневзвешенному индивидуальному индексу цены (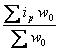), то есть AR показывает среднюю меру изменения количества товаров в результате изменения цен;

2) по значению AR можно непосредственно оценить, что растет быстрее или медленнее: изменение объемов опережает изменение цен или наоборот. Так, если AR > 1, то можно утверждать, что:

- рост объемов опережает рост цен;

- снижение объемов меньше падения цен;

- объемы растут, а цены падают.

Если AR < 1, то имеет место обратный процесс;

3) в практическом использовании AR более понятен и прост, чем индекс ковариации, так как, участников рынка абсолютно не интересует, больше индекс Пааше индекса Ласпейреса или меньше. Их интересует, что растет быстрее – объемы продаж или цены на товары, то есть спрос или предложение, сложившиеся на рынке;

4) расчет AR значительно проще расчета I_COV , что снижает трудоемкость исследований;

5) являясь общей внутренней структурной характеристикой индексных систем Пааше и Ласпейреса, AR дает дополнительную информацию об индексах и тем самым расширяет аналитические возможности статистика по их исследованию. В частности, как видно из рисунка 1, индексные системы (1) и (2) могут быть представлены с помощью AR в следующем виде:

                                             I_q^L                        I_p^L

 

                                (6)

 

I_q^P                        I_p^P

На основе выше изложенного можно сделать вывод, что проблема выбора индексной системы сводится к обоснованию взаимоувязки AR либо с индексами цены, в одном случае, либо с индексами объема, в другом, а не с индексами цены и объема как в случае использования I_COV. Следовательно AR концентрирует внимание на внутренних (I_p^L × AR = I_q^L и I_p^P × AR = I_q^P) проблемах индексных систем, не нарушая баланс между ними, что упрощает, как показали исследования, проблему выбора единственной формулы общего индекса.

В заключение отметим, что в работах некоторых авторов имеются попытки анализа влияния агрегатов «» и «» на формирование общего индекса. Например, в широко известном индексе Ф. Дивизиа встречается взаимосвязь величин «» и «» в виде квадрата суммы, а именно:

,                                      (7)

но, как пишет Ковалевский Г.В., «… ни одна из статистических служб Запада так и не решилась «аппроксимировать» индекс Дивизиа». Р. Аллен также писал, что для получения индексов формы Пааше и Ласпейреса требуется вычисление двух перекрёстных величин «» и «». При этом Р. Аллен указывает, что при вычислении общего индекса, как правило, пользуются обеими перекрестными оценками. Венгерский статистик П. Кёвеш обращал внимание на взаимоотношение величин «» и «» друг к другу, отмечая, что их отношение дает один и тот же результат, и что простота, с которой можно получить это отношение «…без всяких проблем взвешивания, наводит на мысль о том, что оно заслуживает особого внимания».

Таким образом, предлагаемый авторами подход позволяет говорить об отношении величин «» и «» друг к другу как об универсальной внутренней структурной характеристике индексных систем, заслуживающей глубокого изучения и имеющей ясный экономический смысл. При этом применение AR в аналитических целях дает новый толчок для развития индексной теории.