К ВОПРОСУ ОПТИМИЗАЦИИ РАЗМЕЩЕНИЯ РЕМОНТНОГО

ПРОИЗВОДСТВА

 

Шиловский В.Н., Саливоник А.В., Кутырев Е.В., Гольштейн Г.А.

(ПетрГУ, г.Петрозаводск, РФ)

 

The article presents a procedure and mathematical model with continuous variables on the optimization of repair work disposal.

 

Математические модели системы авторемонтного производства являются нелинейными из-за нелинейной зависимости технико-экономических показателей производств от их мощности [1]. Для решения задач большой размерности, характерной для задач развития и размещения авторемонтного производства, могут быть использованы методы нелинейного программирования или более простые приближенные методы, дающие удовлетворительные по точности результаты при меньших затратах труда и материальных средств [2].

Существует два основных метода решения задачи оптимизации размещения ремонтных производств транспортных машин. Первый метод предусматривает разработку математических моделей с дискретными переменными, второй – с непрерывными переменными по размещению и развитию ремонтно- обслуживающих производств.

Первый метод основан на сведении производственно-транспортной задачи к транспортной. Он весьма эффективен для решения задач с дискретными переменными при сравнительно небольшом числе возможных вариантов развития и размещения ремонтно-обслуживающих пунктов.

Второй метод позволяет решать задачи с непрерывными переменными практически любой размерности. Необходимым условием его использования является отсутствие ограничений на возможность расширения производств.

Для решения задач по оптимизации размещения ремонтно-обслуживающих пунктов для ремонта и технического обслуживания территориально распределенной лесозаготовительной и лесотранспортной техники возможно применение второго метода, когда мощность пунктов технического сервиса (ПТС) заранее не фиксируется, а определяется в ходе решения задачи, для чего строиться итерационный процесс.

В общем виде задача формулируется следующим образом. Задано территориальное распределение потребности в ремонтно-обслуживающих воздействиях. Пусть  – индекс пункта-поставщика ремонтного фонда ,  – потребность i-го потребителя в ремонте,  – индекс пункта технического сервиса . Удельные приведенные затраты  на технические воздействия на j-ом пункте технического сервиса задаются как функция объема производства ПТС.

Стоимость транспортирования одного объекта для технического воздействия от i-го потребителя на  j-й пункт технического сервиса и обратно задается матрицей:

.

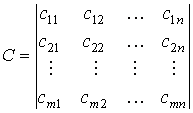Обозначим переменную , представляющую число объектов технических воздействий, поставляемых i-м потребителем j-му ПТС. Требуется определить оптимальную структуру системы технических воздействий, учитывающую размещение и мощность пунктов технического сервиса, и распределение между ними ремонтного фонда.

Математическая модель оптимизации системы организации и осуществления технических воздействий может быть представлена в виде:

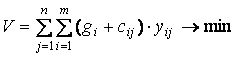.                                                                 (1)

В качестве ограничения минимально допустимую мощность ПТС устанавливают исходя из условия экономической целесообразности существования такой ПТС. Максимальная мощность ПТС может быть принята равная суммарной потребности в ремонте:

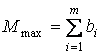.                                                                                             (2)

Выражение (2) предполагает в качестве возможного варианта  создание одного ПТС, удовлетворяющего всю потребность в технических воздействиях определенного числа потребителей в масштабе района, региона.

На интервале  выбираем шкалу мощностей , промежутки между соседними значениями которых определяем исходя из требуемой точности расчетов. В качестве нулевого приближения берутся произвольные, принадлежащие принятой шкале числа .

Для выполнения вычислений может использоваться матрица, форма которой представлена в таблице 1.

 

Таблица 1 – Матрица для расчетов оптимального варианта размещения ПТС

Потребители технического сервиса	Пункты технического сервиса					Объемы технического сервиса
	1	…	j	…	n
1		…		…
…	…	…	…	…	…	…
i		…		…
…	…	…	…	…	…	…
m		…		…
Мощность ПТС		…		…

Для минимизации функции (1) на первой итерации необходимо провести минимизацию по каждой строке для чего для каждого i выбрать , для которого  минимально и положить:

 для  и  для .

Суммируя по столбцам, получаем:

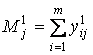.                                                                                               (3)

Значения  округляются до ближайших значений, принадлежащих шкале М и по найденным  перевычисляем зависящих от них величины .

Процесс итерации заканчивается, когда на (k+1)-м шаге получим:

.                                                                                               (4)

Оптимальное решение для k-го шага итерационного процесса и является решением задачи.

 

Литература

1. Дехтеринский Л.В. Проектирование авторемонтных предприятий: Учебное пособие  / Л. В. Дехтеринский, Л.А. Абелевич, В.И. Карагандин и др. – М.: Транспорт, 1981. – 218 с.

2. Шахнес М.М. Современные направления проектирования предприятий для автомобильного транспорта / Под ред. М. М. Шахнеса – М: Транспорт, 1982. – 368 с.