Математическая модель процесса качения пневматического колеса по деформируемому грунту

 

Лазарев В.В. (БГИТА, г. Брянск, РФ)

 

The mathematical model for calculation by a method is developed iterations on the COMPUTER of process swing a pneumatic wheel. On a deformable ground, using for this  purpose known. Dependences between loading on a ground and his deformation.

 

Для современного состояния теории качения колеса по деформируемому грунту характерно наличие значительного числа методических подходов к решению задач связанных с процессом взаимодействия колесного движителя с грунтом. Сложность рассматриваемого процесса из-за неоднородности и нестабильности параметров грунта обуславливает приближенность любых аналитических решений. В этой связи в данном случае более целесообразно применение метода абстрагирования, чем применение строгих теоретических обоснований. Такой подход обеспечивает возможность для определения параметров контакта колес с грунтом использовать известные математические зависимости, дающие результаты расчета, как это отмечается в работе [1], достаточно близкие к действительности.

Расчетная схема процесса взаимодействия колеса с грунтом, в которой, как это предложено целым рядом исследователей выделяются две характерные зоны контакта колеса с грунтом – плоские и кривошипные (рисунок 1).

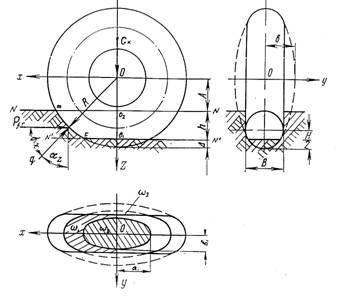
Рисунок 1 – Расчетная схема процесса взаимодействия пневматического колеса  с грунтом

 

При этом приняты следующие допущения.

1) Площадь S_пл плоской зоны контакта колеса с грунтом представлена в виде эллипса с полуосями «» и  (см. рисунок 1). Из треугольников AOB и  следует  , , где R- свободный радиус колеса; R_пр - радиус протектора шины; ∆- радиальная деформация шины в плоской зоне контакта колеса с грунтом.

Поскольку для реальных соотношений величин , R_пр и ∆ у существующих шин произведение 2R_пр∆, а тем более 2R∆>>∆ ², то  с погрешностью расчета не более 1-2% величину ∆ ² из под знака радикала можно исключить, что позволяет значительно упростить вывод расчетных зависимостей. При этом рассматриваются два случая.

а) Случай А, когда прогиб ∆ шины не превышает максимальный  прогиб ее протектора (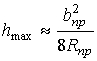). В этом случае .

б) Случай Б, когда прогиб . В этом случае принимается,  что  ширина плоской зоны имеет предельную величину равную ширине  протектора.

2) Геометрическую форму и размеры площади S_кр проекции криволинейной  зоны контакта колеса с грунтом на горизонтальную плоскость N-N представим в виде полуразности площади эллипса с полуосями L_к  и , где  b_к - ширина контакта колеса с грунтом на поверхности колеи и площади эллипса плоской зоны контакта (см. рисунок 1).

Для определения b_к воспользуемся зависимостью полученной Я.С. Агейкиным на основе обработки экспериментальных данных [2].

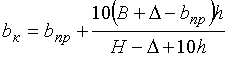                                        ,                                      (1)

где  В и Н – соответственно ширина и глубина профиля шины; h – глубина колеи.

3) Среднее давление q_кр в криволинейной зоне контакта колеса с грунтом, как это предложено в работе [1], принимается равным среднему давлению q в плоской зоне, соответствующему глубине погружения колеса на .

4) Условно принимается, что плоская зона контакта колеса с грунтом по отношению к колесу является твердой опорной поверхностью. При таком допущении значение ∆, на основании зависимости для определения радиуса качения пневматического колеса по твердой опорной поверхности, представим в следующем виде

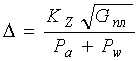,                                                (2)

где - константа шины, отражающая влияние ее конструктивных параметров на величину ∆;  - нормальная нагрузка на плоскую зону контакта колеса с грунтом;  - атмосферное давление; - избыточное давление воздуха в шине.

5) Форму и размеры площади проекции криволинейной зоны контакта колеса с грунтом на плоскость ZOY, величиной которой необходимо  располагать при определении силы сопротивления грунта качению колеса, представлены в виде прямоугольника с высотой равной глубине колеи и шириной b [1].

                                                                        (3)

  В соответствии с принятыми допущениями нормальные нагрузки на плоскую зону G_пл и криволинейную G_кр зоны контакта колеса с грунтом можно представить в следующем виде.

Для случая А:            ;                       (4)

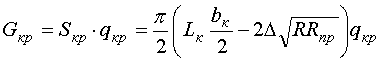.            (5)

Для случая Б: 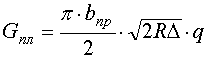                     ;                                    (6)

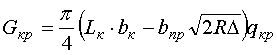                                ,                      (7)

где - длина полухорды окружности с радиусом R.

Решая зависимости (4) и (6) совместно с зависимостью (2) после преобразований получим:

- для случая А: 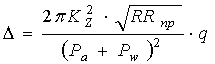                  ;                                         (8)

- для случая Б: 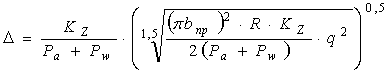               (9)

На основании полученных выше результатов уравнения равновесия вертикальных сил, действующих на колесо при его качении по грунту без учета силы , можно представить в следующем виде:

- для случая А 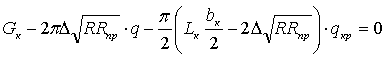               (10)

- для случая Б 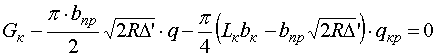  ,  (11)

где ; .

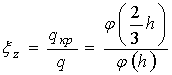Каждое из уравнений (9) и (10) содержит четыре неизвестных: ∆, q, q_кр и h. Поскольку их значения взаимосвязаны, то решения этих уравнений можно выполнить, используя метод итерации (приближения) с помощью ЭВМ.

Для достижения этой цели, задавшись шагом счета глубины h колеи, приняв, например, ∆h= 0,001 м, каждый цикл счета на ЭВМ следует выполнять в следующей последовательности:

1) .

2) . Если 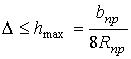, то значения ∆ определяется по зависимости (8), если иначе, то по зависимости (9).

3) .

4) .

5) 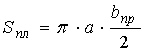, если . Если иначе, то .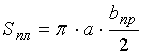

6) .

7) .

8) , если , иначе

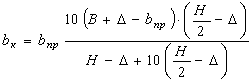
9) .

10) .

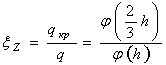11) .

12) .

13) .

Расчет проводится до тех пор, пока не будет соблюдаться следующее равенство

 ,                                      (14)

где - величина нормальной нагрузки приходящейся на плоскую зону контакта колеса с грунтом, соответствующая принятому шагу счета .

Выполнение этого равенства свидетельствует о справедливости результатов, полученных  в последнем цикле счета.

Предлагаемая методика расчета позволяет для определения параметров качения пневматического колеса по грунту использовать практически любую известную зависимость между нагрузкой и нормальной осадкой грунта.

Воспользуемся, например, для этой цели весьма распространенной степенной зависимостью Винклара-Гесретерна-Бернштейна

,                                                  (15)

где с и μ – параметры грунта.

Представим зависимость (15) в следующем виде

,

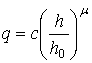где h₀ – базовая деформация грунта.

Если принять, что h₀ = 0,01 м, то такое представление зависимости (15) позволяет при расчетах в системе СИ использовать имеющиеся экспериментальные данные с и μ справедливые при размерности q равной кгм/см².

При этом можно записать

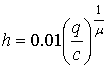, м.                                                (16)

В соответствие с принятой расчетной схемой зависимость для определения силы сопротивления грунта представим в следующем виде

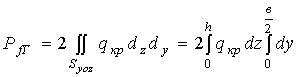,                            (17)

где S_yoz – симметричная половина площади лобового сопротивления качению колеса по грунту; q_кр  = qζ_z -  давление колеса на грунт в криволинейной зоне контакта колеса с грунтом.

Имея в виду,  что в данном случае

,

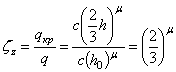после преобразований зависимости (17) приходим к следующему результату

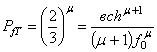.                                      (19)

В качестве следующего примера для определения величин h, P_f  и значения  ζ_z   воспользуемся зависимостью профессора В.В. Кацыгина между нормальным напряжением σ  и  деформацией грунта, представленной в виде функции гиперболического тангенса [2]

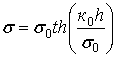,                                            (20)

где σ₀ -  предел прочности грунта; к₀ – коэффициент объемного смятия грунта.

После ряда преобразований зависимости (20) автором настоящей работы получены следующие формулы:

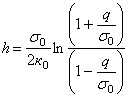;                                       (21)

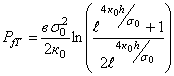;                                   (22)

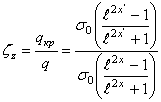,                                   (23)

где  , .

Литература

1. Агейкин Я.С. Проходимость автомобилей/ Я.С.Агейкин. – М.: Машиностроение, 1981. – 232 с.

2. Тракторы: теория. Учебник для студентов  вузов по спец. «Автомобили и тракторы» / В.В.Гуськов, Н.Н. Веляев, Ю.Е. Атаманов и др. Под общ. ред В.В.Гуськова. – М.: Машиностроение, 1988. – 376 с.