ПРИМЕНЕНИЕ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ ПРИ определениИ ОПТИМАЛЬНого количества ПУНКТов сбора платы за проезд на платном участке дороги
Власов С.С., Гасилов В. В. (ВГАСУ, г. Воронеж, РФ),
Бондарев Б.А. (ЛГТУ, г. Липецк, РФ)
Modelling of mass service systems. Use of mass service system at definition of necessary quantity of points for gathering of a payment for travel on a paid site of road.
Системы массового обслуживания — это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания.
С позиции моделирования процесса массового обслуживания ситуации, когда образуются очереди заявок (требований) на обслуживание, возникают следующим образом. Поступив в обслуживающую систему, требование присоединяется к очереди других (ранее поступивших) требований. Канал обслуживания выбирает требование из находящихся в очереди, с тем, чтобы приступить к его обслуживанию. После завершения процедуры обслуживания очередного требования канал обслуживания приступает к обслуживанию следующего требования, если таковое имеется в блоке ожидания.
Цикл функционирования системы массового обслуживания подобного рода повторяется многократно в течение всего периода работы обслуживающей системы. При этом предполагается, что переход системы на обслуживание очередного требования после завершения обслуживания предыдущего требования происходит мгновенно, в случайные моменты времени.
Примерами систем массового обслуживания могут служить:
• посты технического обслуживания автомобилей;
• посты ремонта автомобилей;
• станции технического обслуживания автомобилей;
• аудиторские фирмы;
• телефонные станции и т. д.
Основными компонентами системы массового обслуживания любого вида являются:
• входной поток поступающих требований или заявок на обслуживание;
• дисциплина очереди;
• механизм обслуживания.
В качестве основных критериев эффективности функционирования систем массового обслуживания в зависимости от характера решаемой задачи могут выступать:
• вероятность немедленного обслуживания поступившей заявки;
• вероятность отказа в обслуживании поступившей заявки;
• относительная и абсолютная пропускная способность системы;
• средний процент заявок, получивших отказ в обслуживании;
• среднее время ожидания в очереди;
• средняя длина очереди;
• средний доход от функционирования системы в единицу времени и т.п.
Предметом теории массового обслуживания является установление зависимости между факторами, определяющими функциональные возможности системы массового обслуживания, и эффективностью ее функционирования. В большинстве случаев все параметры, описывающие системы массового обслуживания, являются случайными величинами или функциями, поэтому эти системы относятся к стохастическим системам.
Случайный характер потока заявок (требований), а также, в общем случае, и длительности обслуживания приводит к тому, что в системе массового обслуживания происходит случайный процесс. По характеру случайного процесса, происходящего в системе массового обслуживания (СМО), различают системы марковские и немарковские. В марковских системах входящий поток требований и выходящий поток обслуженных требований (заявок) являются пуассоновскими.
Пуассоновские потоки позволяют легко описать и построить математическую модель системы массового обслуживания. Данные модели имеют достаточно простые решения, поэтому большинство известных приложений теории массового обслуживания используют марковскую схему. В случае немарковских процессов задачи исследования систем массового обслуживания значительно усложняются и требуют применения статистического моделирования, численных методов с использованием ЭВМ.
Независимо от характера процесса, протекающего в системе массового обслуживания, различают два основных вида СМО:
• системы с отказами, в которых заявка, поступившая в систему в момент, когда все каналы заняты, получает отказ и сразу же покидает очередь;
• системы с ожиданием (очередью), в которых заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь и ждет, пока не освободится один из каналов.
Системы массового обслуживания с ожиданием делятся на системы с ограниченным ожиданием и системы с неограниченным ожиданием.
В системах с ограниченным ожиданием может ограничиваться:
• длина очереди;
• время пребывания в очереди.
В системах с неограниченным ожиданием заявка, стоящая в очереди, ждет обслуживание неограниченно долго, т.е. пока не подойдет очередь.
Все системы массового обслуживания различают по числу каналов обслуживания:
• одноканальные системы;
• многоканальные системы.
Приведенная классификация СМО является условной. На практике чаще всего системы массового обслуживания выступают в качестве смешанных систем. Например, заявки ожидают начала обслуживания до определенного момента, после чего система начинает работать как система с отказами.[1]
В нашем случае для определения необходимого количества пунктов сбора платы за проезд на платном участке дороги (с) рассматривается многоканальная система массового обслуживания с ожиданием. Процесс массового обслуживания при этом характеризуется следующим: входной транспортный поток является пуассоновским с интенсивностью Инт прог. Средняя продолжительность обслуживания одной машины в пункте сбора равна — 1/μ, которая определяется на основе статистических данных работы пункта. За единицу времени принята 1 минута, соответственно, интенсивность входного потока λ = Инт прог/525600. Режим функционирования того или иного пункта не влияет на режим функционирования других пунктов сбора системы, причем длительность процедуры взимания платы каждым из пунктов является случайной величиной, подчиненной экспоненциальному закону распределения. Также необходимо отметить, что средняя продолжительность пребывания машины в системе ограничена Ws и условием стационарности системы является:
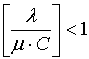 .
.
Определим необходимое количество пунктов сбора платы за проезд на платном участке, исходя из того, что вероятностные характеристики функционирования в стационарном режиме многоканальной СМО с ожиданием и неограниченной очередью определяются по следующим формулам [2]:
ρ = λ / μ (1)
• среднее число клиентов в очереди на обслуживание
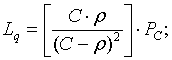 (2)
(2)
• среднее число находящихся в системе клиентов (заявок на обслуживание в очереди)
LS = Lq + ρ (3)
• средняя продолжительность пребывания клиента (заявки на обслуживание) в очереди
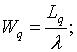 (4)
(4)
• средняя продолжительность пребывания клиента в системе
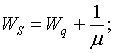 (5)
(5)
![]() ;
; ![]() ;
;
![]() ; (6)
; (6)
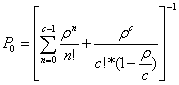 (7)
(7)
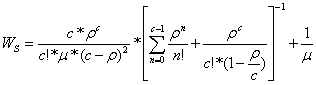 . (8)
. (8)
Принимая во внимание, что общая максимальная плата за проезд по всем категориям автотранспорта меньше или равна суммарной экономической выгоде пользователей платного дорожного объекта по сравнению с альтернативным проездом, получаем:
(Дi x Ri) / (365 x Инт прог) ≤ Эi, (9)
где Ri – норма дисконта i-того года;
Инт прог – прогнозируемая интенсивность на новой платной дороге;
Эi - суммарная экономическая выгода пользователей платного дорожного объекта по сравнению с альтернативным проездом i-того года.
Дi = Зсод i + Зстр/N + Кi + Пс i + ДДi + Чпi+(Зшсодi+Зшстр/N)*с, (10)
где Зсод i – эксплуатационные затраты i-того года;
Зстр - затраты на реализацию проекта строительства новой или модернизации существующей автодороги;
N – количество лет концессии;
Кi – проценты, выплачиваемые по банковским кредитам i-того года;
Пс i - расходы на социальные нужды - представлены в форме доли чистой прибыли, нормируемой от инвестированного капитала или от стоимости ОПФ i-того года;
Ддi – выплата дивидендов i-того года;
ЧПi – чистая прибыль i-того года;
Зшсодi+Зшстр/N – удельные затраты на содержание и строительство 1 пункта сбора платы за проезд;
с – количество пунктов сбора платы.
Определим из неравенства с:
с ≤ (Эi х 365 х Инт прог) / Ri – Зсодi – Зстр/N –Кi – Псi – Ддi – Чпi . (11)
Зшсодi+Зшстр/N
Исходя из условия стационарности системы и того, что с (необходимое количество пунктов сбора платы за проезд на платном участке) – натуральное число (сЄN), получаем систему ограничений для выбора количества пунктов:
ρ< с ≤ (Эi х 365 х Инт прог) / Ri – Зсодi – Зстр/N –Кi – Псi – Ддi – Чпi . (12)
Зшсодi+Зшстр/N
В зависимости от выбранного вида пунктов сбора платы будут различаться удельные затраты и, соответственно, их количество, необходимое для оптимальной средней продолжительности пребывания машины в системе (Ws), которая является одним из признаков привлекательности для пользователей платной автодороги.
Для обоснования экономической эффективности строительства платных объектов дорожного хозяйства предлагается использовать разработанные методы определения стоимости платных услуг, которые предусматривают определение оптимальной платы за проезд, приемлемой для пользователей и инвесторов и позволяющей реализовать проект в установленные договором концессии сроки.
Литература
1. Гасилов В.В. Экономико-математические методы и модели в строительстве. ВГАСУ, 1998 г.
2. Таха Х. Введение в исследование операций: В 2-х книгах. Кн. 2. Пер. с англ. – М.: Мир, 1985.