ПРОБЛЕМА ДОСТИЖЕНИЯ ТОЧНОСТИ ДОЗИРОВАНИЯ МАТЕРИАЛОВ
Поляков С.И. (ВГЛТА, г.Воронеж, РФ)
In the article the rating of accuracy of dosage of cement is carried conducted by metering devices of AD-series at manual and computer process control, experimental data of a dynamic error of dosage are parsed.
Управление технологическим процессом взвешивания и
дозирования материалов связано с обеспечением требуемой точности дозирования,
что представляло всегда острую техническую научную проблему. В частности, в промышленности
стройматериалов при приготовлении бетонных смесей используются весовые
дискретные дозаторы, для которых погрешность взвешивания составляет: для
цемента и воды 
2 %, для инертных заполнителей 2,5 %. На самом деле фактическая погрешность значительно превосходит
паспортную и зависит от способности оператора, обслуживающего дозаторы
бетоносмесительных установок, в буквальном смысле, «ловить» заданный вес дозы
при перемещении стрелки по лимбу циферблатных указателей. Управление дозаторами
в ручном режиме «грубого-точного» взвешивания при досыпке материала связано с частыми
срабатываниями релейно-контактной аппаратуры, оно приводит к ее неисправной
работе и быстрому износу. В этой ситуации говорить о качественном приготовлении
смесей по составу не приходится.
Проблеме управления дозированием уделяется большое внимание
в периодических изданиях, в частности, в журнале «Современные технологии
автоматизации», где публикуются статьи по внедрению современных автоматизированных
систем управления, контрольно-измерительных систем управления процессами
весодозирования и приготовления бетонных смесей. В них описывается элементная
база, характеристики систем, особенности программного обеспечения. А вопросы,
касающиеся того, каким образом достигается требуемая точность, мягко говоря, корректно
обходятся. Общие фразы типа «адаптация к скоростным характеристикам
материальных потоков» или «расчет, насколько раньше должен закрыться дозатор,
чтобы погрешность была в допустимых пределах» [1] не отражает суть
математического обеспечения, принятого разработчиками таких систем в качестве
способов дозирования. Не ясно, как в динамике удалось достичь приведенной
погрешности дозирования 1,5% [1].
В настоящее время традиционный подход в решении проблемы достижения требуемой точности заключается в нахождении упреждения на последующие циклы дозирования через усреднение погрешностей предыдущих взвешиваний. Рассматривается дискретное дозирование с динамической погрешностью. При этом образуется дискретный случайный ряд погрешностей предыдущих циклов дозирования. В проблеме прогнозирования погрешность в
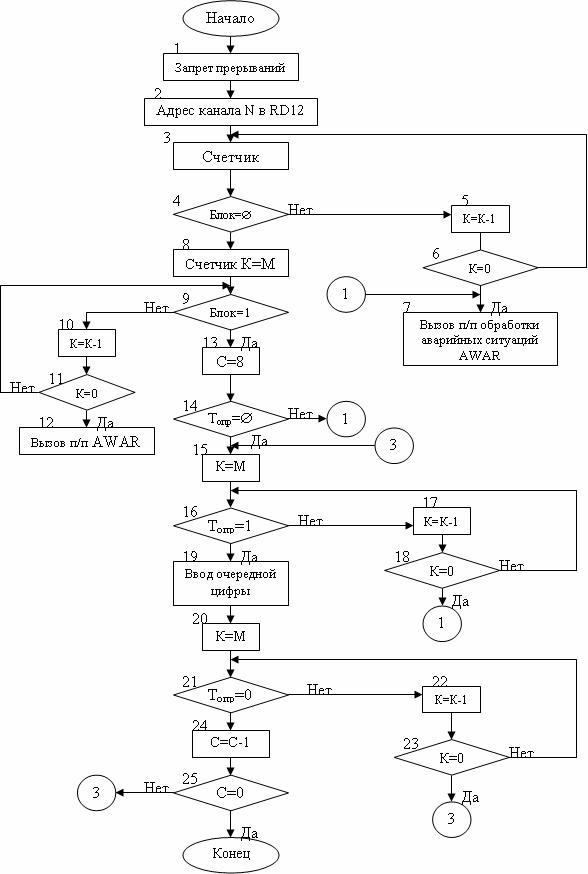
Рисунок 1- Алгоритм подпрограммы взвешивания компонентов WES
текущий цикл дозирования и предудущие погрешности позволяют вычислить прогнозируемую погрешность путем их усреднения, то есть получить упреждение на последующие n циклов дозирования. Эта процедура относится к классу моделей скользящего среднего. Подобные модели используются в АСУ дозированием компонентов бетонных смесей. Часть этого подхода реализована в алгоритме подпрограммы взвешивания компонентов, представленном на рисунке 1.
Заключение
Для создания автоматизированной системы управления дозированием и учёта расхода сыпучих тел с целью описания хода технологического процесса необходимо проведение соответствующего математического моделирования, учитывающего технологические особенности и возмущающие воздействия на процесс дозирования, который предполагается рассмотреть как совокупность технологических операций со своими математическими методами и моделями.
Процесс дозирования носит стохастический характер, так
как определяется рядом неизвестных факторов. Здесь требуется применение теории
вероятностей для определения модели процесса. Точность дозирования
непосредственно связана с прогнозом погрешности и с ее упреждением l на n циклов
дозирования. Следовательно, требуется по модели процесса получить прогноз
(прогнозирующую функцию) 
, для которого выполняется требование:
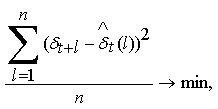
где
- истинное значение погрешности в 
цикл дозирования.
Образуемый ряд циклов дозирования одного материала на одном и том же весовом оборудовании является нестационарным и не имеет естественного среднего значения.
Стохастическая модель процесса дозирования, для которой прогнозирование экспоненциально взвешенным скользящим средним является оптимальным, относится к классу нестационарных процессов – «процессов авторегрессии – проинтегрированного скользящего среднего (АРПСС)» [2].
Литература
2. Бокс Д., Дженкинс Г. Анализ временных рядов: Прогноз и упр. – М.: Мир, 1974. – Вып.1.- 406с.