ХАРАКТЕРИСТИКИ МИКРОПРОФИЛЕЙ ТРЕЛЕВОЧНЫХ ВОЛОКОВ, ОПРЕДЕЛЯЮЩИЕ ДИНАМИЧЕСКОЕ УПЛОТНЕНИЕ ПОЧВЫ

 

Григорьев И.В. (ГЛТА им. С.М. Кирова г. Санкт-Петербург)

 

They аre вrought statistical features got as a result of studies an mikroprofils of skidding portages.

 

Движение трелевочной системы сопровождается непрерывным изменением сил взаимодействия движителя и древесины с опорной поверхностью. Эти изменения обуславливаются как изменчивостью сил сопротивления качению, так формой, размерами и чередованием неровностей волока, которые преодолевает трелевочная система. В своей совокупности эти силы вызывают колебания подрессорных и неподрессорных масс системы, изменения крутящего момента на ведущих колесах и скорости движения системы. Совокупность неровностей формируют опорной поверхности, характеризующие случайные изменчивости вдоль оси волока. Поэтому при математическом моделировании на современном уровне используются возможности статистического метода, которые не исключают, а дополняют детерминированные методы исследования динамически мобильных систем.

         В теории случайных функций и ее приложении к исследованию динамических систем [1-4] случайный процесс ξ(t) определяется как случайная функция неслучайного параметра t, величина которого в каждом tT являются случайными величинами. ГОСТ 21878-76 рассматривает случайный процесс как семейство векторных или скалярных случайных величин, зависящих от его мерного параметра, имеющего размерность времени. Следовательно случайный процесс является обобщением понятия случайное событие, а случайная величина может принять любое заранее неизвестное значение. В отличие от события случайная величина характеризует количественный результат опыта.

         В настоящее время расширяется применение в исследовании тракторных, сельскохозяйственных, и других машин статистической динамики, которая базируется на теории случайных функций и автоматического регулирования [1-5]. К наиболее ранним исследованиям лесотранспортных машин с использованием статистической динамики можно отнести работы проф. Жукова А.В.

         Применение статистической динамики при исследованиях различных мобильных систем в основном сводится к исследованию динамики систем и нагруженности элементов конструкции. При движении трелевочной системы трелевочный трактор преодолевает значительные неровности трелевочного волока; при этом происходят интенсивные колебания подрессоренной и неподрессоренной масс системы и, как следствие, происходит динамическое уплотнение почвы. На динамическое уплотнение почвы влияют колебания трелевочной системы в вертикальной, поперечной и продольной плоскостях, следовательно, необходимо иметь математические модели неровностей как по длине волока, так и превышение неровностей одной колеи по отношению к другой.

         В опубликованных работах по исследованию лесосечных машин и трелевочных волоков в ограниченном объеме, без систематизации, приводятся математические модели только неровностей продольного профиля; отсутствует обоснование шага квантования и длительности эксперимента или длины мерного участка [6-9]. Задача исследования состоит в определении статистических характеристик неровностей продольного и поперечного профилей трелевочных волоков с обоснование шага и длины мерного участка волока.

         Многочисленные исследования микропрофилей дорог показали, что неровности можно рассматривать, как случайный стационарный процесс, обладающий эргодичностью [2, 3], а эмпирическое распределение ординат и экстремумов высот неровностей показывают, что описывающие их законы близки к нормальным. Следовательно, случайные функции, моделирующие микропрофиль можно считать гаусовскими [3, c. 70]. Аналогичные заключения применительно к неровностям трелевочных волокам и силам сопротивления движения трелевочных систем сделали исследователи лесотранспортных машин [6, 7].

         Для получения характеристик микропрофиля опорной поверхности применяются прямой и косвенный методы. Прямой метод базируется на применении различных измерительных средств, от простых, например нивелир, до сложных измерительных систем. Косвенный метод сводится к определению не микропрофиля, а измерению, регистрации и обработки реакции динамической системы на воздействия неровностей пути. Оба метода имеют достоинства и недостатки, анализ которых позволяет предположить, что косвенный метод может давать завышения дисперсии [10, 11]. В отличие от автомобиля или сельскохозяйственного агрегата, трелевочный трактор трелюет древесину по относительно короткому трелевочному волоку, имеющему значительные неровности, следовательно, применение существующих измерительных систем микропрофиля, длина которых достигает 24 м [12], исключается.

         При математическом моделировании неровностей опорной поверхности ее профилируют и получают случайную функцию x(l) пути L. Профилеграммы Z_l(L) обрабатываются на ЭВМ с целью получения дисперсии D_Z, корреляционной функции R_Z(l) и спектральной плотности S_z(ω); при этом аргумент l будет иметь размерность длины (м), а аргумент ω – размерность м^-1.

         Для сравнительного анализа удобно использовать безразмерные величины и параметры. В статистической динамике в качестве безразмерной характеристики неровностей используют нормированную корреляционную функцию ρ(l), которую в теории вероятностей называют коэффициентом корреляции [13]

.

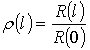Переход в описании функции неровностей от аргумента L к аргументу t (время) основан на том, что при единичной скорости продвижения по волоку численные значения аргументов совпадают и для обеих функций будет связующими время (t), путь (L) и скорость (v) продвижения относительно микронеровностей [2, 3]

.

Следовательно, в статистических характеристиках случайных функций микропрофиля переход от аргумента l к аргументу τ=Δt базируется на равенстве их числовых значений при единичной скорости.

         Наиболее часто экспериментальные корреляционные функции апроксимируются выражением [2, 4, 6, 7]

,

где: α и β – коэффициенты.

Для учета скорости движения коэффициенты α и β при единичной скорости (v=1м/с) умножают на заданную скорость v, то есть:

,        .

При переходе от аргумента l к временному аргументу τ используют связь τ=l/v.

         В производственных условиях были измерены отклонения неровностей семи волоков, один из которых относится к лесовозной дороге, так как имел незначительные неровности, по высоте от условной горизонтальной плоскости с фиксированием этих отклонением через 0,5-1,0м. Такой метод в статистике называют методом случайных ординат [7]. Методами, изложенными в известных монографиях [13, 14] с применением ЭВМ, по статистическим рядам неровностей были определены законы распределения и нормированные корреляционные функции. Законы распределения неровностей получены по длине волока, т.е. продольный профиль и по превышению одной колеи над другой, т.е. поперечный профиль. Анализ законов распределения неровностей показал, что все они имеют нормальное распределение с изменением статистик в довольно широком диапазоне, особенно это относится к продольному профилю.

         В монографии А.А. Силаева рекомендуется, при оценке воздействия неровностей на колебания динамических систем, все проселочные дороги разбить на три класса: к первому отнести дороги, у которых средняя квадратичная высота неровностей σ_н≤10 см; ко второму – дороги с σ_н=10-20 см; к третьему – дороги с σ_н>20 см. В исследованиях А.А. Силаева только одна из 12 исследованных дорог имела неровности σ_н>24 см.

         Следует отметить, что трелевочный волок, в отличие от проселочных дорог должен быть подготовлен, видимо, поэтому в наших исследованиях даже очень тяжелый волок, с точки зрения сопротивления движению трелевочной системы, имел σ_Н=14,8.

         Исследования семи волоков позволяют классифицировать трелевочные волоки по неровностям на три класса: к первому отнести волоки σ_Н≤5 см, ко второму – волоки с σ_Н=5-10 см и к третьему – волоки с σ_Н> 15 см.

         Статистики М и σ позволяют определить коэффициенты вариации v_П, характеризующие степень изменчивости процесса.

         Значение v_П позволяет при заданной величине вероятности Р и допустимой ошибки ε по «Номограмме достаточно больших чисел» [14] определить необходимое минимальное число отсчетов или число измерений, а, следовательно, при заданном шаге квантования – минимальную длину мерного участка волока. Анализ корреляционной функции и спектральной плотности продольных и поперечных микропрофилей семи волоков показал, что коэффициент вариации или степень изменчивости процесса находится в пределах от 19 до 60, по таблице «Достаточно больших чисел» число отсчетов или изменений в опыте должно быть не менее 384 опыта, т.е. при шаге квантования 0,5 м длина мерного участка волока должна быть не менее 192 м. Коэффициенты аппроксимации корреляционных функций находятся в пределах α=0,5-1,0с^-1, β=1,3-1,8с^-1.

Выводы

         Полученные статистические характеристики микропрофиля в продольной и поперечной плоскостях трелевочных волоков и лесовозной дороги, позволяющие определить диапазон изменения значений статистических законов распределения и коэффициентов уравнений аппроксимации случайных функций, которые необходимы при исследовании динамического уплотнения почвогрунтов лесосеки трелевочными системами.

 

Литература

1. Пугачев В.С. Теория случайных функций и ее применения к задачам автоматического управления. М.:
2. Силаев А.А. Спектральная теория подрессоривания транспортных машин. М. 1963.
3. Яценко Н.Н. Форсированные полигонные испытания грузовых автомобилей. М.: Машиностроение. 1984. 328с.
4. Лурье А.Б. Статистическая динамика сельскохозяйственных агрегатов. М.: Колос. 1970. 376с.
5. Бриннер В.А., Карамос А.А., Палеев П.П. и др. Динамика проходческих комбайнов. М.: Машиностроение. 1977. 226 с.
6. Жуков А.В., Леонович И.И. Колебания лесотранспортных машин. Минск, БГУ им. Ленина, 1973. 240 с.
7. Анисимов Г.М. Условия эксплуатации и нагруженность трансмиссии трелевочного трактора, М.: Лесная промышленность. 1975. 168 с.
8. Добрынин Ю.А. Исследования параметров трелевочных волоков как системы случайных волоков В сб. «Машины и орудия для механизации лесозаготовок». Межвузовский сборник научных трудов. Вып. 5. 1976, С. 17-20.
9. Пархиловский И.Г. Исследование вероятностных характеристик поверхности распространенных типов дорог. //Автомобильная промышленность, 1968. № 8. С.18-22.
10.  Щетина В.А. Грачев Е.В. Косвенный метод исследования статистических характеристик микропрофиля автомобильных дорог. //Автомобильная промышленность, 1969. № 12. С.11-14.
11. Щуплянов В.С. Колебания и нагруженность трансмиссии автомобиля. –М.: Транспорт, 1974. 328 с.
12. Митропольский А.К. Техника статистических исчислений. М.: Физлеатгиз, 1961. 576 с.
13. Митков А.П., Кардашевский С.В. Статистические методы в машиностроении. М.: Машиностроение, 1978. 360 с.
14.  Венцель Е.С. Теория вероятности. М.: Наука, 1964. 576 с.