Площадь контакта в зацеплении цилиндрических зубчатых колес с учетом шероховатости

 

Тихомиров П.В. (БГИТА, г.Брянск, РФ)

 

Influence of a roughness in a zone of a contact on structure of the area of contact of gearwheels is considered. The technique of definition of the actual area of contact that allows revealing tribological characteristics of transfer by gearing is resulted.

 

Для оценки контурной площади контакта с учетом шероховатости используем известную формулу Г. Герца, в соответствии с которой полуширина площадки касания двух выпуклых тел (цилиндров) определяется выражением

 

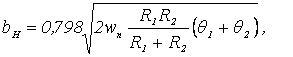
где w_n − удельная нагрузка, Н/мм; R₁, R₂ − радиусы сопряженных цилиндров, мм; 2_1,2 =(1-<_1,2)/Е_1,2, <_1,2 − коэффициенты Пуассона, Е_1,2 − модули упругости материалов шестерни и колеса).

Как известно, приведенная зависимость справедлива для гладких (без шероховатости) несмазанных поверхностей сопряженных деталей. Наличие шероховатого слоя дает основание считать, что его физико − механические характеристики будут отличаться от свойств основного материла. Структура этого слоя характеризуется множеством микрогеометрических высотных и шаговых параметров, определяемых ГОСТ 2789−73. Одним из комплексных параметров, отражающим особенности структуры шероховатого слоя, является параметр D − фрактальная размерность (1<D<2). При этом, чем больше величина D, тем сложнее профиль. Для прямой линии D=1. Известно, что между параметрами шероховатости и свойствами шероховатого слоя имеется определенная связь. Введем понятие эффективного модуля упругости, связанного с фрактальной размерностью следующим соотношением:

,                                                 (1)

где Е − модуль упругости основного материала; H − коэффициент, входящий в показатель степени (в первом приближении H=1); g − относительное сближение поверхностей (0< g <1).

Введение эффективного модуля E_eff позволяет модифицировать формулу Герца, заменив в упругой константе 2 модуль упругости основного материала на величину эффективного модуля.

Тогда полуширина площадки контакта с учетом шероховатости будет равна

               (2)

 

Для стальных колес, поверхности которых имеют одинаковую шероховатость, выражение (2) запишем в виде

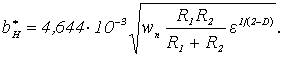                             (3)

 

Как видно из приведенных зависимостей при увеличении сближения эффективный модель растет, приближаясь к модулю упругости основного металла.

Расчетная оценка полуширины площадки контакта с учетом шероховатости зависит от относительного сближения, которое в неявном виде входит в уравнения (2) и (3). Примем следующее допущение. Шероховатый слой представим в виде своеобразного покрытия одинаковой толщины, равной D=Rmax₁+Rmax₂. Здесь толщина слоя D равна сумме наибольших высот неровностей первого и второго тел. Этот слой обладает переменной жесткостью, зависящей от относительного сближения. Такой подход позволяет найти относительное сближение из выражения

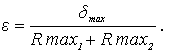                                          (4)

 

С другой стороны для упругого контакта можно записать

                                          (5)

где Rnp=R₁R₂/(R₁+R₂).

 

Приравняв выражения (5) и (2), запишем

 

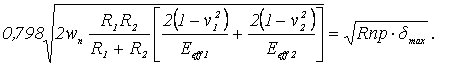
Решим полученное уравнение относительно g, приняв n₁=n₂=n и Е₁=Е₂=Е.

 

Тогда

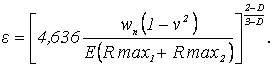                                (6)

 

Таким образом, приведена методика определения фактической площади контакта, основанная на фрактальных представлениях о шероховатой поверхности, что позволяет выявить трибологические характеристики пар трения.