ИССЛЕДОВАНИЯ КОЛЕБАНИЙ В КОНИЧЕСКОМ
ДИФФЕРЕЦИАЛЕ МЕТОДОМ ИМИТАЦИОННОГО МОДЕЛИРОВНИЯ

 

Ражиков В.Н.  (БГТУ «Военмех», Санкт-Петербург, РФ)

 

The result of studying the processes of vibration in the bevel gear differential are tated in the given paper.

 

В ходе разработки электромеханического привода  силового гироскопа, в состав которого был включен конический дифференциал, возникла необходимость оценить влияние конструктивных параметров на колебательные процессы. Конический дифференциал использовался для резервирования электродвигателя и быстроходной части кинематической цепи привода, поэтому при функционировании резервный вход у дифференциала был загружен. При исследовании было решено рассмотреть только крутильные колебания в дифференциале, т.к. эти колебания могли оказать влияние на кинематику привода. Отмеченные упрощения позволили свести систему дифференциальных уравнений (1) к системе из четырех дифференциальных уравнений второго порядка, дополняемой одним уравнением связи. Источником внешнего возбуждения колебаний в дифференциале считалась кинематическая погрешность зацеплений «сателлит- колесо».

Как отмечалось ранее, для решения системы дифференциальных уравнений, описывающих колебательные процессы в коническом дифференциале, используют метод начального интегрирования типа Кутта-Мерсона. Однако использование его в виде программы ЭВМ неудобно при решении задач оптимизации конструктивных параметров. Это связно с тем, что процесс расчета разбивается на этапы: 1) задание начальных условий; 2) непосредственно расчет на ЭВМ; 3) обработка данных вычисления; 4) решение об изменении того или иного начального условия при увязке его с параметрами конструкции дифференциала. Значительно удобнее решать задачи оптимизации методом имитационного моделирования. Для этой цели была использована интегрированная математическая система МАТЛАБ 6.1. с разделом SIMULINK.

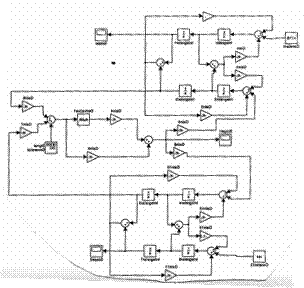
Рисунок 1- Имитационная модель колебаний дифференциала

 

На рис.1 показана имитационная модель колебаний конического дифференциала. В такой модели изменение  того  или иного коэффициента системы уравнений значительно упрощено. Задание функции кинематической погрешности зубчатых пар сателлит-колесо осуществлялось с помощью генератора сложных сигналов. Это позволило приблизить задаваемую в модели кинематическую погрешность к реальной, т.к. в сигнале были объединены накопленная и местная кинематические погрешности. В процессе решения можно наблюдать изменение параметров колебаний во времени, влияя на процессы развития резонансов и затухания. На рис.2 показано полученное при  имитационном моделировании изменение усилия в зацеплении зубьев сателлита и центрального колеса.

 

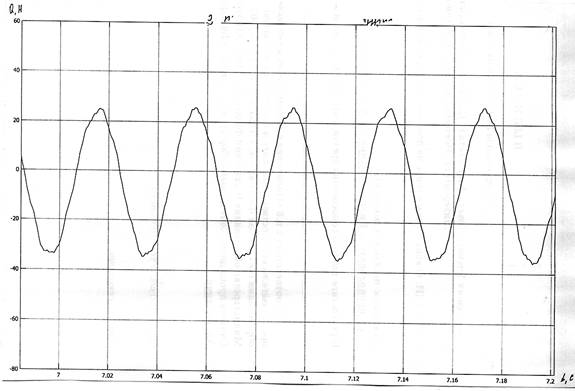
Рисунок 2- Колебания действующей нагрузки в зацеплении зубьев сателлита и центрального колеса