МАТЕМАТИЧЕСКИЕ МОДЕЛИ БРЕВЕН
СИБИРСКОЙ ЛИСТВЕННИЦЫ
Герасимова М.М., Ветшева В.Ф. (СибГТУ, г. Красноярск, РФ)
Models of Siberian larchwood logs were built and was made a comparison of their factual volumes with standard meanings.
Математические модели пиловочных
бревен лиственницы сибирской были построены по данным обмера 2500 бревен на
Новоенисейском ЛХК. При обмере бревен учитывалось место их вырезки из хлыста.
Каждое бревно делили на 10 секций равной длины, 
, где L
– длина бревна. В конце каждой секции, начиная от комля, производили замеры
диаметров бревен - 
.
Полученные регрессионные
зависимости (1) – (4) характеризуют изменение относительных диаметров 
по
относительной длине бревен 
. Они достаточно точно
выражаются полиномом второй степени:
,
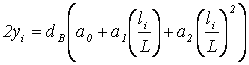где 
- диаметр бревна в месте
измерения, см;
dВ - диаметр бревна в вершинном торце, см;
li - расстояние от комля до места измерения, см;
L – длина бревна, м;
- параметры регрессии.
Для комлевых бревен
,
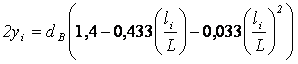(1)
для срединных
,
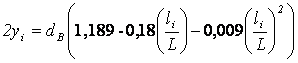(2)
для вершинных
.
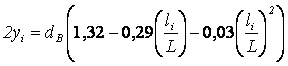(3)
Для всего сырья
.
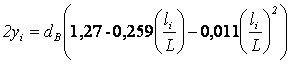(4)
Для всех уравнений показатель корреляционной связи R=0,99. Проверку статистической значимости каждого регрессионного уравнения проводили по F-критерию Фишера, сравнивая фактическое (Fфакт) и табличное (Fтабл) значения.
Fфакт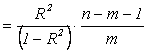
,
где 
- коэффициент
детерминации, показывающий долю вариации результа-
тивного признака 
, объясняемую вариацией
фактора 
;
n – число наблюдений;
m – число параметров
при переменной 
.
Для всех уравнений регрессии коэффициенты детерминации R2 равны 0,98, n=11, m=2. Следовательно,
Fфакт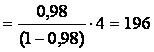
.
Табличное значение критерия (Fтабл) при степенях свободы k1=2, k2=8
и уровне значимости 
равно 4,46. Так как Fфакт> Fтабл,
то уравнения являются статистически значимыми, следовательно, полученные
математические модели адекватны исходным данным.
Графическое изображение зависимостей (1)–(4) представлено на рисунке 1.
 |
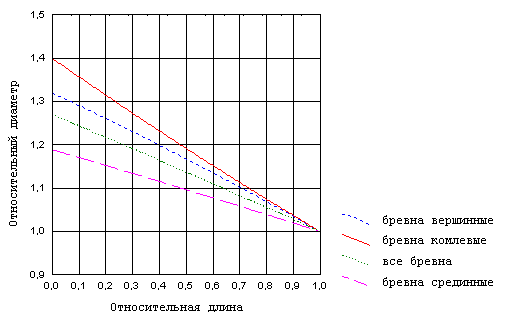Рисунок 1 – Модели образующих бревен
По этим моделям были определены фактические объемы бревен Vф:
Vф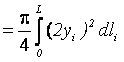
.
Поскольку в ГОСТ 2708 стандартные объемы бревен даны без учета их места вырезки, дополнительно разработаны модели бревен разных групп диаметров независимо от их расположения в хлыстах. Для средних диаметров в каждой учтенной группе с шагом 10 см модели имеют вид:
при длине бревен 4,0…5,25 м
dср= 18 см
,
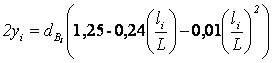dср= 28
см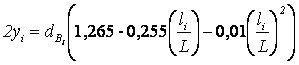 
,
dср= 38
см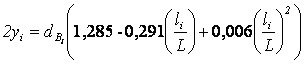 
,
dср= 48
см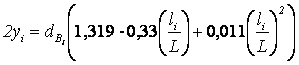 
;
при длине бревен 5,5…6,5 м
dср= 18
см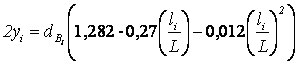 
,
dср= 28
см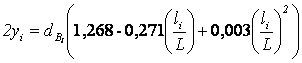 
,
dср= 38
см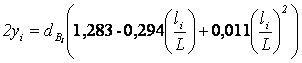 
,
dср= 48
см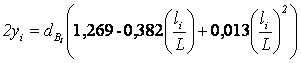 
.
В таблице 1 представлены
фактические объемы бревен в выделенных группах, имеющих средний диаметр 18, 28,
38 и 48 см, и дано их сравнение со стандартными значениями (Vст). Коэффициент 
определен по
отношению фактического объема бревен к стандартному.
Таблица 1 – Фактические и стандартные объемы бревен
|
dср, см |
L=4…5,25 м |
L=5,5…6,5 м |
||||||||
|
Кср |
Lср |
Vф |
Vст |
|
Кср |
Lср |
Vф |
Vст |
|
|
|
18 |
1,25 |
4,2 |
0,136 |
0,127 |
1,07 |
1,28 |
6 |
0,2 |
0,2 |
1 |
|
28 |
1,27 |
4,25 |
0,338 |
0,306 |
1,1 |
1,27 |
6,1 |
0,485 |
0,45 |
1,08 |
|
38 |
1,28 |
4,2 |
0,624 |
0,562 |
1,11 |
1,28 |
6 |
0,889 |
0,82 |
1,084 |
|
48 |
1,32 |
4,1 |
1,001 |
0,84 |
1,19 |
1,37 |
6 |
1,532 |
1,3 |
1,18 |
Из таблицы следует, что с увеличением диаметра бревен этот коэффициент возрастает.
Проведенные исследования показали,
что фактический объем бревен превышает стандартное значение при длине L=4…5,25 м на 7…19 %, а при длине L=5,5…6,5
м - на 8…18 %. По этим данным, зная стандартный объем бревен, можно находить их
фактические значения: Vф=
Vст. Это позволит предприятиям с большей
точностью определять резервы комплексного использования древесины.
Литература
1. Петровский В.С. Оптимальная раскряжевка лесоматериалов. – М.: Лесн. пром-сть, 1989.-288 с.
2. Ветшева В.Ф., Малькевич М.В. Рациональный раскрой пиловочного сырья. - Красноярск, 1993.-150 с.
3. Ферстер Э., Ренц Б. Методы корреляционного и регрессионного анализа. М.: Финансы и статистика, 1983.-302 с.