ИССЛЕДОВАНИЕ ПРОЦЕССА ПРЕССОВАНИЯ ТОПЛИВНЫХ БРИКЕТОВ ИЗ ДРЕВЕСНЫХ ОТХОДОВ

 

Брагин А.В., Ганапольский С.Г. (ВятГУ, г.Киров, РФ)

 

The expression is received, for definition of pressure in any section of a briquette during pressing the crushed wood on stamp press in the closed matrixes

 

Значительная часть отходов лесопильной и деревообрабатывающей промышленности, включая отходы окорки, по той или иной причине не находит технологического применения. Одним из простейших и наиболее эффективных способов подготовки древесных отходов к утилизации является изготовление топливных брикетов методом прессования. Процесс прессования древесных отходов требует дополнительных теоретических разработок для оптимизации основных факторов влияющих на качество брикетов.

В процессе прессования измельченной древесины на штемпельных прессах в закрытых матрицах работа затрачивается на преодоление остаточной и упругой деформации частиц измельченной древесины соответствующего объема, сил внутреннего трения между отдельными частицами и внешнего трения о стенки матрицы, а так же на удаление воздуха из материала и матрицы.

Рассмотрим влияние сил трения на процесс прессования брикета в матрице (рисунок 1).

Рисунок 1 – Распределение давлений при прессовании брикета в закрытой матрице

 

При прессовании начальная высота слоя материала Н₁ уменьшится до Н₂, а сила на штемпеле возрастет от 0 до Р₂. Давление при этом изменяется по кривой АВ. По окончании процесса прессования давление в объеме брикета меняется от р₂ на штемпеле до р₀ на упоре по кривой ВС, уравнение которой можно получить аналитически. Рассмотрим сечение брикета на расстоянии Н от упора, в котором давление равно р. В сечении, отстоящем от сечения Н на бесконечно малом расстоянии dH, давление равно р+dp. На брикет действуют следующие силы: силы бокового распора, направленные горизонтально к стенкам матрицы, силы трения материала о стенки матрицы, направленные вертикально вниз, сила сопротивления материала, направленная вертикально вверх и сила прессования, направленная вертикально вниз.

Суммарная сила трения определяется выражением:

,                                             (1)

где f – коэффициент трения;

e – коэффициент бокового распора;

p – давление прессования в рассматриваемом сечении;

u – периметр брикета;

dH – высота слоя.

При допущении, что давление р по сечению брикета одинаково, условие равновесия сил в слое брикета запишется в следующем виде:

,                          (2)

где s – площадь поперечного сечения брикета.

После преобразования получим

.                                             (3)

В идеальном случае, при р₂»р₀ и допущении, что по сечению матрицы s и u величины постоянные, значение коэффициента e  можно считать неизменным. Вследствие незначительной разности температур матрицы на участке Н₂ значение f также принимается неизменным. На основании сказанного выражение  будет величиной постоянной. Тогда уравнение (3) можно представить

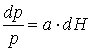.                                                (4)

После интегрирования и логарифмирования получаем

,                                               (5)

где C – постоянная интегрирования.

Для определения постоянной С положим, что Н=0, тогда р=р₀ и уравнение (5) перепишется в виде:

.                                                 (6)

Тогда текущее значение р определяется из выражения:

.                                               (7)

где р₀ – давление на упоре;

Н – текущее значение высоты брикета, считая от упора.

Полагая в уравнении (7) Н=Н₂, получим:

.                                               (8)

По значению р₂ определяется давление на упоре:

.                                             (9)

Если отсчет расстояния до произвольного сечения вести не от упора, а от штемпеля, то уравнение (7) примет вид:

.                                           (10)

Таким образом, получено выражение для определения давления в любом сечении брикета, которое является аналитическим уравнением кривой ВС.