ИСПОЛЬЗОВАНИЕ ПЛАСТИЧНЫХ СМАЗОЧНЫХ МАТЕИАЛОВ ПРИ РАСЧЕТЕ И ПРОЕКТИРОВАНИИ МЕХАНИЗМОВ

Ражиков В.Н., Бильдюк Н.А. (БГТУ "Военмех" Санкт-Петербург, РФ)

 

The results of studying the processes in partial elastogydrodinamic lubrication of greases are stated in the given paper.

При проектировании механизмов с пластичными смазочными материалами необходимо знать несущую способность смазки, величину ее расхода в зоне трения и сопротивление относительному перемещению взаимодействующих деталей. Пластичные смазки являются неньютоновскими жидкостями, отсюда вытекает и особенность их работы в зоне трения. Нанесенный на сопряженную поверхность пластичный смазочный материал в начальный  период работы оттесняется из рабочей зоны, при этом оставшееся количество смазки, определяемое адгезией, как правило, не обеспечивает полного разделения контактирующих деталей. Таким образом, основной период они работают в условиях полужидкостного трения, при котором необходимо учитывать параметры взаимодействующих поверхностей (микрорельеф, свойства материала и другие).

Анализ течения пластичного смазочного материала в зоне контакта шероховатых поверхностей проводился методом осредненного течения, использовавшегося Патиром и Чженом для Ньютоновских жидкостей. В основу было положено уравнение течения пластичных смазок типа Гершеля-Балкли. В результате было выведено модифицированное уравнение Рейнольдса:

 

                      (1)

 

Где  - коэффициенты расхода напорного течения,  - параметры, зависящие от характера образования ядер в смазочном слое;  - аналог пластической вязкости смазочного материала;  - среднее давление на площадке условного объема смазки; n - показатель нелинейности в уравнении течения пластичной смазки Гершеля-Балкли;  - номинальная толщина слоя смазки, разделяющего трущиеся поверхности; - суммарная скорость качения сопряженных поверхностей;  - максимальная скорость скольжения;  - фактическая величина толщины смазочного слоя, включающая значения высот взаимодействующих микронеровностей; R_q - среднеквадратическое отклонение высот микронеровностей; - коэффициент расхода сдвигового течения.

При выводе принимались следующие допущения : 1) смазка несжимаемая; 2) рассматриваются номинальные поверхности двух цилиндров бесконечной длины; 3) соприкосновение и деформирование отдельных микронеровностей не приводит к изменению геометрии слоя в окрестности этих выступов; 4) микронеровности характеризуются малыми углами наклона; 5) течение пластичного смазочного материала описывается уравнением Гершеля-Балкли.

Уравнение (1) не решается даже численными методами, так как n - действительное число в диапазоне от 0 до 1. Для приведения его к виду, имеющему решение, был разработан метод послойного течения, который  предполагает замену уравнения Гершеля-Балкли системой уравнений Шведова-Бингама. В результате уравнение (1) удалось заменить системой дифференциальных уравнений эллиптического типа:

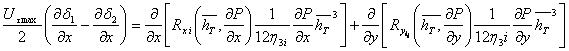(2)
где i = 1…m.

 

Здесь    ,    - коэффициенты, зависящие от характера образования ядер в смазочном слое;   - текущие значения высот микронеровностей контактирующих поверхностей;   -  вязкость рассматриваемого слоя смазки.

Уравнения (2) было решено численными методами и найдены значения коэффициентов расхода напорного течения . При его решении численно воспроизводились трехмерные шероховатости с заданными среднеквадратическим отклонением высот микронеровностей, коэффициентом затухания автокорреляционной функции и коэффициентом анизотропии. Значение коэффициентов расхода      используют далее при решении эластогидродинамических задач для полужидкостного трения при пластичной смазке.

Исследования показали, что решение многих практических задач о смазывании зубчатых передач, подшипников качения и скольжения сводится к плоскому случаю. Кроме этого, течение пластичного смазочного материала считается ламинарным, стационарным, изотермическим. Для решения эластогидродинамических задач использовались, помимо уравнения Рейнольдса (1) в одномерном виде, уравнение зазора между номинальными недеформированными поверхностями трения, уравнение упругих деформаций в зоне контакта, аналитическое выражение для коэффициента расхода напорного течения; уравнение давления, воспринимающего контактирующими микронеровностями; уравнения зависимости вязкости и напряжения сдвига пластичной смазки от температуры и давления.

Решение позволяет определить параметры течения пластичной смазки в условиях эластогидродинамического трения, такие как эпюры гидродинамического давления и давления, воспринимаемого микронеровностями, сопротивление перемещению, расход смазочного материала. Полученные результаты использовались при создании механических приводов космических аппаратов.