РАСЧЕТ КОЛЬЦЕВЫХ ВИБРОИЗОЛЯТОРОВ ИЗ МАТЕРИАЛА МР С ПОМОЩЬЮ ЭКВИВАЛЕНТНОГО МОДУЛЯ УПРУГОСТИ
Пономарев Ю.К., Уланов А.М. (СГАУ, г.Самара, РФ)
Цзян Хунюань, Ся Юйхун (ХПИ, г.Харбин, КНР)
The calculation of ring-shape vibration isolators made of metal rubber (MR material) by the help of equivalent elastic modulus are considered in this paper. A conception of equivalent elastic modulus allows to use for calculation a standart software ANSYS.
В современных виброзащитных системах широко применяются виброизоляторы из материала МР, получаемого холодным прессованием спирали из стальной проволоки. Такие виброизоляторы имеют высокие демпфирование, прочность и стойкость к воздействию окружающей среды (масел, кислот, радиации, вакуума, солнечного света и т.д). Во многих виброизоляторах из МР упругодемпфирующие элементы выполнены в виде кольца (рис.1) \1\. Поперечное сечение кольца обычно имеет вид прямоугольника с размерами b x h . Представляет интерес применение для расчета упругих характеристик таких колец современных конечноэлементных программных средств. Для этого необходимо знать модуль упругости материала МР.
Рисунок 1- Кольцевой виброизолятор из материала МР
Деформация 
в направлении оси Y (в
рассматриваемом случае она совпадает с осью болтов) кольца из линейного
материала определяется зависимостью 
, где 
- сила, 
- радиус
кривизны кольца, 
- модуль упругости, 
- момент
инерции сечения кольца вокруг оси Х \2\. Отсюда 
(1) ,
где 
- жесткость кольца
без учета силы трения в направлении оси Y около положения равновесия 
.
Материал МР и кольцо из него обладают нелинейными
характеристиками, однако около положения равновесия упругая линия кольца близка
к линейной, и можно экспериментально определить 
(2),
где T и 
- отрезки, отсекаемые
петлей гистерезиса соответственно на осях силы и деформации (рис.2).
Рисунок 2- Петля гистерезиса кольцевого виброизолятора
Исходный радиус кривизны кольца 
после установки
элементов крепления с шириной 
меняется. Если бы свободные
участки кольца имели форму полукруга, радиус их кривизны был бы 
. Реальный
радиус больше 
, но меньше , и можно предположить
(3)
Таким образом, для определения эквивалентного модуля
упругости материала МР в направлении оси Y достаточно экспериментально
определить петлю гистерезиса кольца, найти на ней отрезки T и , рассчитать
значение 
по
формуле (2), значение R по формуле (3) и определить Е по формуле (1).
Модуль Е зависит также от относительной плотности
материала МР 
, где 
- плотность материала
МР, 
-
плотность стали. Первоначально были исследованы кольца с 
.
Параметры исследованных колец и полученное значение
модуля Е приведены в таблице 1. Ширина элемента крепления для всех колец 
.
Таблица 1
|
Кольцо |
|
|
|
|
|
|
1 |
0.20 |
9.5 |
7.3 |
5.0 |
10.50 |
|
2 |
0.20 |
14.5 |
7.5 |
5.0 |
9.15 |
|
3 |
0.20 |
17.5 |
7.8 |
5.0 |
11.14 |
Среднее значение
, отклонения от него могут быть
связаны как с погрешностью определения радиуса R, так и с технологическими
отклонениями параметров материала МР при изготовлении колец.
Параметры материала МР при сжатии различны в направлении силы прессования и в направлении, перпендикулярном силе прессования материала. Однако можно предположить, что эти различия будут не столь велики при работе материала МР на изгиб, происходящей при деформации кольца. Поэтому можно воспользоваться эквивалентным модулем упругости в направлении оси Y для расчета упругих характеристик колец в направлении двух других осей.
Для расчета при помощи метода конечных элементов
необходим также коэффициент Пуассона 
. Его значение было определено
при деформации образца из МР в виде цилиндрической втулки высотой 35 мм,
внешним диаметром 25 мм и внутренним диаметром 10 мм. Экспериментально получено
.
Поскольку коэффициент Пуассона для МР очень мал, погрешности в его определении
не окажут существенного влияния на результаты расчета.
Для проверки возможности расчета упругой характеристики кольца при помощи эквивалентного модуля упругости Е были проведены расчеты упругих деформаций колец при помощи конечноэлементной программы ANSYS. Сравнение расчетных деформаций и экспериментально полученных упругих линий для колец из МР различного размера приведены на рис.3-7.
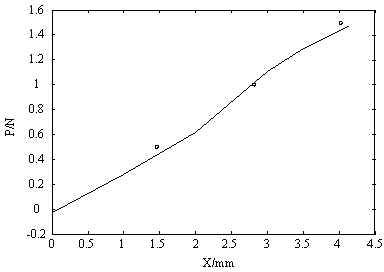
Рисунок 3- Упругая линия кольца 1 в направлении оси Х
Рисунок 4- Упругая линия кольца 1 в направлении оси Y
Рисунок 5- Упругая линия кольца 1 в направлении оси Z
Рисунок 6- Упругая линия кольца 3 в направлении оси Х
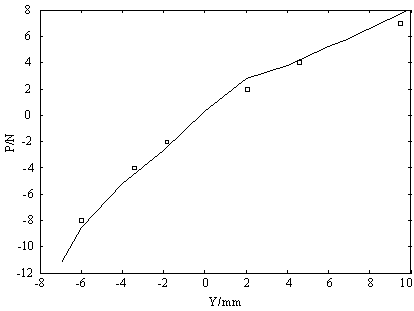
Рисунок 7- Упругая линия кольца 3 в направлении оси Y
Видно, что погрешность определения деформации (и,
соответственно, жесткости) по упругой линии обычно не превышает 10%. Поскольку
определенная по упругой линии жесткость 
используется обычно для
расчета резонансной частоты виброизолятора 
(где m – масса виброзащитной
системы), погрешность в 10% при определении жесткости приводит к погрешности 5%
при определении резонансной частоты, что можно считать удовлетворительной
точностью.
Таким образом, упругая линия любого кольцевого виброизолятора из материала МР может быть рассчитана с удовлетворительной точностью методом конечных элементов, с использованием однажды полученного при помощи эксперимента эквивалентного модуля упругости.
Литература
1. Чегодаев Д.Е., Мулюкин О.П., Колтыгин Е.В. Конструирование рабочих органов и оборудования из упругопористого материала МР. СГАУ: Самара, 1994. Ч.1 – 156 с. Ч.2 – 100 с.
2. Тимошенко С.К. Сопротивление материалов. Том 1. М.: Наука.– 1965. – 363 с.