ЗАВИСИМОСТЬ ОБЪЁМА БЕССУЧКОВОЙ ЗОНЫ БЕРЁЗОВОГО СТВОЛА ОТ ТАКСАЦИОННЫХ ПОКАЗАТЕЛЕЙ ДРЕВОСТОЕВ
Петровский В.С., Головнёв В.Н., Попов В.К. (ВГЛТА, г. Воронеж, РФ)
The results of research of influencing of timber taxations parameters on her quality indicators
При разработке САПР решающих проблемы проведения рубок ухода за лесом, требуются математические зависимость различных размерных, качественных и количественных показателей древостоев от их таксационных показателей. В данной статье приводится один из вариантов нахождения объёма безсучковой зоны берёзового ствола в зависимости от полноты и возраста древостоя.
Порядок нахождения модели выглядит следующим образом.
Объём безсучковой зоны можно представить как объем усечённого конуса. Объем конуса вычисляется как:
(1)
Далее нам потребуется найти некоторые математические зависимости.
По таблицам из
[1] найдем зависимость между высотой и возрастом для каждого бонитета в отдельности
. Для получения
достаточной точности модели в нашем случае это будет полином 4-й степени:
(2)
Таблица 1-Коэффициенты для полинома (1) по бонитетам
|
Бонитет |
A0 |
A1 |
A2 |
A3 |
A4 |
|
Ia |
-1.7 |
0.897624 |
-0.010384 |
0.000065 |
1.777389E-7 |
|
I |
-1.2 |
0.774355 |
-0.008696 |
0.000055 |
-1.573427E-7 |
|
II |
-1.825 |
0.704206 |
-0.007702 |
0.000046 |
-1.209207E-7 |
|
III |
-2.158333 |
0.618831 |
-0.006949 |
0.000044 |
-1.29662E-7 |
|
IV |
-1.616667 |
0.885484 |
-0.009867 |
0.000057 |
-1.340326E-7 |
Для 1а бонитета t = 10…100; 1 и 2 бонитетов t = 20…100; 2. 3 и 4 бонитетов t = 20…90.
По результатам сравнения отклонение расчетных значений средних высот от опытных данных колеблется в пределах 0 - 3%. Средний процент отклонения в пределах одного бонитета не превышает 0.6%.
По данным из того
же источника (1) найдем зависимость диаметра на высоте груди от высоты 
.
Наиболее
точно эта зависимость описывается в экспоненциальной форме 
(3)
Таблица 2-Коэффициенты для экспоненциального уравнения (3) по бонитетам
|
Бонитет |
A |
B |
|
Ia |
0.287698 |
0.113608 |
|
I |
0.233274 |
0.124091 |
|
II |
0.420933 |
0.128695 |
|
III |
0.631062 |
0.132006 |
|
IV |
0.787047 |
0.139587 |
|
V |
0.847839 |
0.148541 |
По результатам сравнения табличные данные расходятся с расчетными лишь в нескольких случаях более чем на 5%. Поэтому модель с достаточной долей уверенности можно считать адекватной.
Используем уравнение для образующей древесных стволов проф. Петровского В.С. [2]
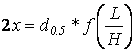(4)
Математическая модель хлыста березы в коре получена с помощью таблиц Тюрина (1):
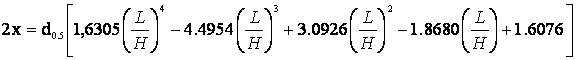(5)
Далее переходим от диаметра на высоте груди к диаметру на половине высоты ствола [3]:
(6).
По данным, представленным в работе [4], получена математическая модель, которая позволяет по входным данным - возрасту и полноте насаждения вычислить высоту до первого живого сучка в относительных величинах (в процентах от общей высоты дерева).
Полученная модель представлена ниже:
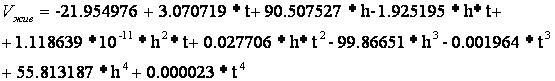(7)
Подставим формулу
(7) в формулу (5) вместо L. Для упрощения обозначим
как k, где H - высота дерева.
Вернёмся к формуле
(1). В нашем случае R это радиус в комле ( 
), а r радиус ствола в месте, где появляется первый сучок (
).
(8)
(9)
Итак, объем безсучковой зоны вычисляется как:
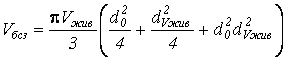(10)
Данная зависимость
выглядит как 
.
Подставляя в уравнение (10)
уравнения (2, 3, 6, 7, 8, 9) получим зависимость вида 
(12)
где 
, H
и Vжив вычисляются по формулам 2 и 7
соответственно;
- вычисляется через
формулу (6) с подстановкой значения 
из
формулы (3).
Литература
1. Тюрин А.В., Науменко И.М., Воропанов П.В., Лесная вспомогательная книжка, 1956.
2. Петровский В.С. Оптимальная раскряжевка лесоматериалов. - 2-е изд., перераб. и доп. - М.: пром-сть, 1989.-288с. ISBN 5-7120-0118-7.
3. Анучин Н.П. Лесная таксация. - М.: Лесная пром-сть, 1982.-552с.
4. Состояние берёзовых насаждений лесостепи ЦЧО, их улучшение и ведение хозяйства в них: Отчёт о НИР за 1969-1970 г. – Воронеж: ВЛТИ, 1970. 311 с.