Напряженное состояние цилиндрических прямозубых колес

НАПРЯЖЕННОЕ СОСТОЯНИЕ ЗУБЬЕВ ЦИЛИНДРИЧЕСКИХ ПРЯМОЗУБЫХ КОЛЕС

Супин В.В., Клоков Д.В. (МТЗ, БГТУ, г. Минск, РБ)

The gear tooth stress analysis investigated in this paper represents an important and typical stress concentration problem which is frequently encountered in gear design practice. The problem of stress concentration at the root of gear solved the boundary element method (BEM).

Создание нового типоразмерного ряда трансмиссий тракторов «Беларус», имеющих жизненный цикл не менее 15-20 лет, требует внедрения новых технологий проектирования, построенных на современных расчетных методах. Зубчатые передачи являются элементами трансформации энергии. К ним предъявляются все более высокие требования в отношении их несущей способности, обусловленные передачей большей мощности в прежних габаритах, повышенным ресурсом, пониженным шумом и они во многом определяют технико-экономические показатели изделия.

Представление о несущей способности эвольвентных зубчатых передач долгое время ограничивалось исследованиями передач, в основу которых положен стандартный исходный реечный контур по ГОСТ 13755-81. Однако практическое исчерпание возможностей улучшения прочностных и качественных показателей заставляет конструкторов все чаще обращаться к поиску новых соотношений параметров зубчатых профилей. В передачах автомобильных трансмиссий находят применение исходные контуры c углами профиля α=14º30´; 17º30´; 22º30´ и 25º. Для высоконапряженных цилиндрических зубчатых колес авиационных редукторов ГОСТ Р 50531-93 устанавливает применение исходных контуров с α=25º при коэффициенте высоты головки зуба =1 и α=28º при =0,9. Все большее применение находят передачи с нестандартным исходным контуром, обеспечивающим коэффициент перекрытия в зацеплении ε_α>2,0 [1].

Применение передач с нестандартным профилем зуба выявило недостаточность известных методик по расчету напряжений в зубьях. Развитие метода граничных элементов (МГЭ) и создание комплекса программ позволило определять напряжения при изгибе зубьев зубчатых колес практически любого исходного контура (нестандартного симметричного, несимметричного и пр.). Выбранное количество и размещение узловых точек на контуре зуба обеспечивает почти аналитическую точность определения максимального напряжения (в пределах долей процента), что существенно выше, чем можно получить МКЭ.

В расчетной практике используется также коэффициент асимметрии цикла r=σ_с/σ_р, равный отношению максимальных напряжений σ_s на сжатой и растянутой переходных кривых зуба, и относительный градиент первого главного напряжения [2]

=-1/σ₁_max (dσ₁/dn),

где σ₁_max – главное напряжение в точке концентрации на контуре; n – нормаль к контуру, проходящая через точку концентрации, производная берется вдоль нормали к переходной кривой.

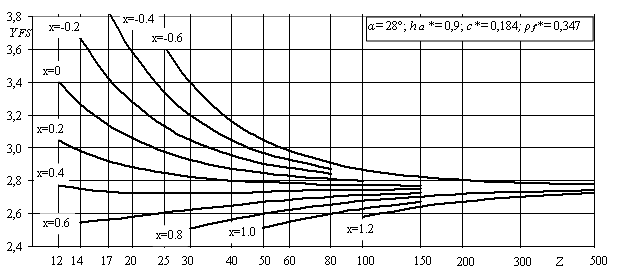
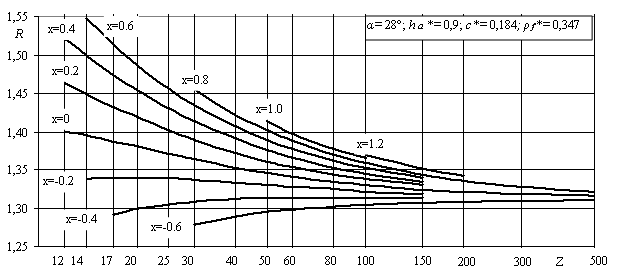
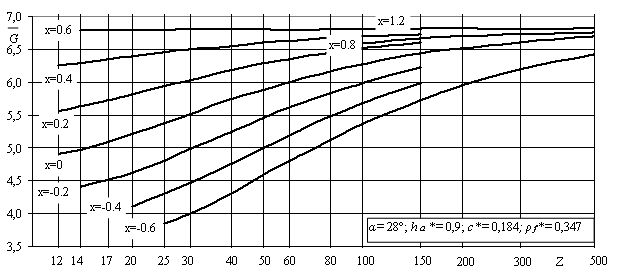
Рисунок 1- Коэффициент формы зуба и концентрации напряжений Y_FS,
коэффициент асимметрии цикла напряжений R, относительный градиент напряжений

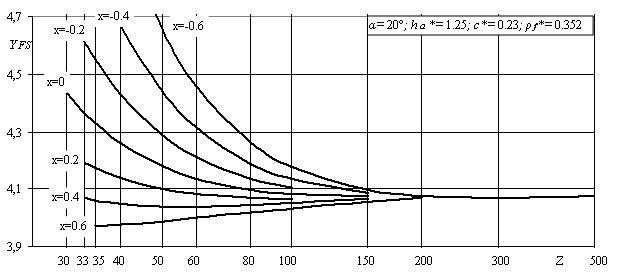
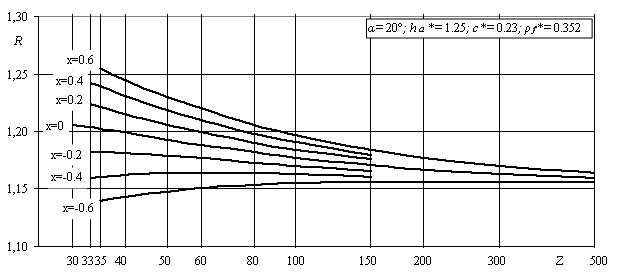
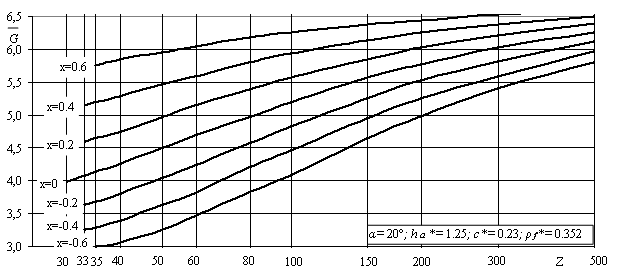
Рисунок 2- Коэффициент формы зуба и концентрации напряжений Y_FS,
коэффициент асимметрии цикла напряжений R, относительный градиент напряжений

Определение коэффициентов Y_FS, r и зубьев, нарезанных инструментом реечного типа, выполнено как для стандартного исходного контура, так и для контуров с полностью скругленной впадиной и профильными углами α=14º30´, 17º30´, 25º при =1, α=28º при =0,9, а также α=20° при =1,25. Диапазон чисел зубьев z=10-500 при коэффициентах смещения x=-0,6 до +1,2. Последний исходный контур испытан в силовых передачах с многопарным зацеплением, что позволило достичь увеличения передаваемой мощности в том же пространственной объеме [1].

На рисунках 1, 2 показаны графики Y_FS , r, для колес с параметрами исходных контуров таблицы (№ 5, 6), где α - угол профиля, - коэффициент высоты головки, - коэффициент радиального зазора, - коэффициент радиуса кривизны переходной кривой. Границы изменения x и z определены при условиях отсутствия подрезания ножки зуба и заострения вершины.

Посредством полиномиальной аппроксимации получены формулы коэффициента, учитывающего форму зуба и концентрацию напряжений Y_FS для указанных выше исходных контуров (табл.).

Таблица - Параметры исходных контуров и формулы коэффициента Y_FS

№	α				Y_FS
1	14º30´	1,0	0,408	0,544	Y_FS=3,96+11,89/z-27,47x/z-0,015x²
2	17º30´	1,0	0,345	0,493	Y_FS=3,62+13,12/z-27,38x/z+0,028x²
3	20º	1,0	0,25	0,38	Y_FS=3,57+10,46/z-23,36x/z+0,038x²
4	25º	1,0	0,203	0,352	Y_FS=3,08+9,85/z-20,76x/z+0,049x²
5	28º	0,9	0,184	0,347	Y_FS=2,70+8,32/z-19,19x/z+0,063x²
6	20º	1,25	0,23	0,352	Y_FS=3,91+15,89/z-30,69x/z+0,29x²

Аппроксимирующие зависимости включены в программный комплекс расчета трансмиссий тракторов «Беларус» на стадии проектирования.

Таким образом, МГЭ выполнен сравнительный анализ напряженного состояния зубьев зубчатых передач нарезанных фрезами с различными исходными контурами. Полученные графики зависимостей Y_FS , r, уточняют и дополняют сведения о напряженном состоянии цилиндрических прямозубых колес при изгибе, способствуют обоснованному выбору геометрии зацепления.

Литература

1. Супин, В.В. Проектирование трансмиссий тракторов «Беларус» с зубчатыми передачами многопарного зацепления как фактор повышения нагрузочной способности / В.В.Супин // Труды БГТУ. Сер II, Лесная и деревообраб. пром-сть. – 2010. Вып. XVIII. – с. 90-95.

2. Серенсен, С.В. Несущая способность и расчет деталей машин на прочность / С.В. Серенсен, В.П. Когаев, Р.Н. Шнейдерович. – М.: Машиностроение, 1975. – 488 с.