ИССЛЕДОВАНИЕ НАПРЯЖЕННОГО СОСТОЯНИЯ
ПЯТНА КОНТАКТА КОЛЕСА И РЕЛЬСА
Воробьев А.А., Сорокин П.Г. (ПГУПС, г.Санкт – Петербург, РФ)
For development of methods of an estimation of reliability of wheels and rails in operation it is necessary to have theoretical and experimental data about the stress – deformed condition of the wheel rail contact spot at the basic hinds of loadings. We have carried gect calculation of a stress contact spot loading on the well axle of 228 kN (23.6 T) we have compared our estimation vales with those performed different pantries.
Взаимодействие колеса и рельса является физической основой движения подвижного состава по железным дорогам. От параметров этого взаимодействия во многом зависят безопасность движения и основные технико-экономические показатели хозяйств пути и подвижного состава. Так, в частности, потери энергии, обусловленные изнашиванием в системе колесо-рельс, составляют 10% - 30% расходуемых на тягу поездов топливно-энергетических ресурсов. Кроме того, расходы на реновацию рельсов и колесных пар составляют немалую часть общих расходов дистанций пути и локомотивных и вагонных депо соответственно. Особенно большие издержки в связи с этими расходами терпят локомотивные депо, поскольку за последние полвека средний срок службы локомотивной колесной пары существенно сократился.
Среди причин, вызвавших в 60-х – 80-х годах прошлого столетия значительное возрастание интенсивности изнашивания колесных пар, следует отметить замену буксовых подшипников скольжения подшипниками качения, увеличение длины и массы поездов, сужение колеи до 1520 мм, введение профиля рельсов (1979г.), предусматривающего двухточечный контакт бандажа с головкой рельса и другие. Все это в совокупности привело к существенному изменению нагруженности зоны контакта, температуры и условий смазывания в этой зоне, а также к изменению среднестатистической скорости скольжения колеса в поперечном относительно головки рельса направлении. Результатом этих изменений стало существенное возрастание интенсивности изнашивания колес подвижного состава, которое, в свою очередь привело к катастрофическим результатам для локомотивного хозяйства: к концу девяностых годов расходы на реновацию колесных пар достигли недопустимо больших размеров.
На рис. 1. и 2. представлены графики заполнения сети железных дорог России закаленными рельсами [1] и диаграммы структуры обточек колесных пар по эксплуатационному парку локомотивов на сети железных дорог Российской Федерации за 1999 и 2002 гг. [2].
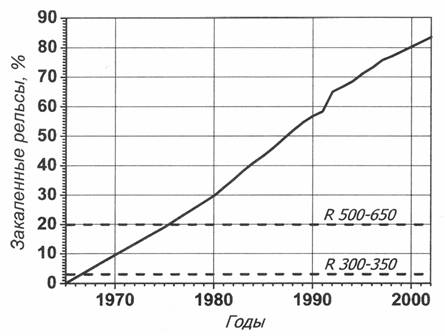
Рисунок 1- Заполнение сети железных дорог России закаленными рельсами
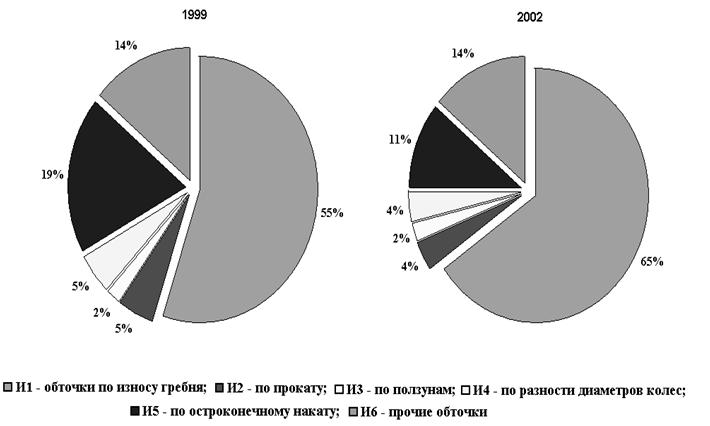
Рисунок 2- Структура обточек колесных пар по эксплуатационному парку
локомотивов на сети железных дорог Российской Федерации за 1999 и 2002 гг.
Из сравнительного анализа диаграмм очевидно, что одновременно с ростом удельного веса объемно закаленных рельсов возрастает и доля обточек по износу гребня. Такая интенсивность износа вызвала рост эксплуатационных расходов в локомотивном и вагонном хозяйствах, связанных с внеплановыми обточками колесных пар, дополнительным приобретением новых бандажей и колес.
Отметим, что обточка колес, при достижении толщины гребня минимального значения, связана со срезом большего объема металла (так называемый технологический износ) с поверхности катания. Это существенно сокращает срок службы бандажа рис. 3.
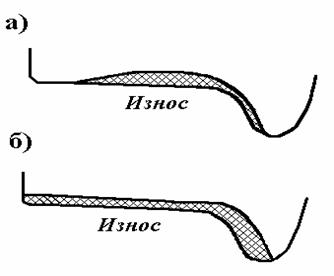
Рисунок 3- Профиль износа гребня:
а – профиль износа 1960 г., б – профиль износа с 1986 г.
С целью снижения интенсивности изнашивания КП до приемлемых значений в последние годы проводится ряд мер технического и организационно-технологического характера [3] (лубрикация, улучшение конструкции пути и подвижного состава, совершенствование геометрии профиля поверхности катания КП и рельсов, повышение качества их металла и т.д.). К сожалению ни одно из этих мероприятий в полном объеме проблемы не решило.
Кардинальное решение вопроса может быть найдено только на базе использования научных знаний в области взаимодействия пары колесо-рельс. Необходимо проведение научно обоснованной модернизации колесных пар с одновременной разработкой мероприятий, обеспечивающих эффективную эксплуатацию и ремонт модернизированных колесных пар.
К технологическим мероприятиям по снижению износа бандажей колесных пар локомотивов относятся следующие мероприятия: исследование процесса взаимодействия колеса с рельсом и воздействие на факторы, влияющие на скорость износа бандажа, конструктивные мероприятия по повышению ресурса, технологические методы упрочнения бандажей, уменьшение трения между бандажом и рельсом, контроль и прогнозирование технического состояния и др. (рис. 4.).
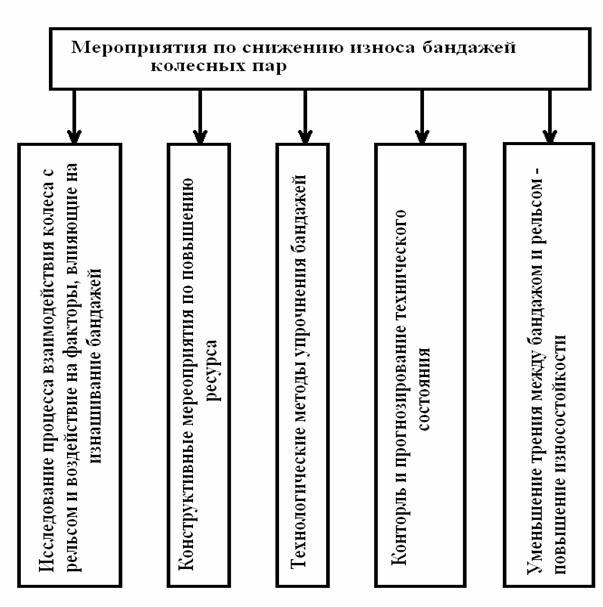
Рисунок 4 - Мероприятия по снижению износа бандажей колесных пар
На износостойкость пары “колесо – рельс” по данным [4] влияют:
твердость материала бандажей, рельс, содержание углерода, структура металлов и
содержание серы. Твердость металла является одним из наиболее существенных
факторов влияющих на износ колес подвижного состава. Внедрение за последнее
десятилетие термической обработки рельсов и придание им твердости 
360 НВ несомненно
сыграло важную роль в улучшении работы железных дорог. Однако с изменением
твердости рельс мер по повышению твердости бандажей предпринято не было. В
результате отношение твердостей стали колеса и рельса оказалось равным 0,75, это
существенно изменило характер износа в паре “колесо – рельс”. В исследованиях
ВНИИЖТа [4], [5] 1960 – 1990х годов отмечалось, что для равной износостойкости
отношение твердости колесного образца к твердости рельсового образца должно
быть порядка 1,2 при проскальзывании до 1%, а
при проскальзывании до 10% – 1,0 – 1,1.
Таким образом, установление оптимальной твердости поверхности
катания колеса представляет собой сложную задачу, решение которой должно осуществляться
системно с учетом, различных параметров, а величина твердости поверхности
катания колес на сегодняшнее время ограничена величиной 
.
Разработка эффективных методов снижения степени износа зависит от наличия методик исследования, оценки параметров контактного взаимодействия пары “колесо – рельс” с помощью численных методов.
Задача контакта качения двух упругих тел, имеющих одинаковые характеристики упругости, как это имеет место для колеса и рельса, может быть представлена раздельно в виде нормальной и тангенциальной задач. Цель первой задачи состоит в определении размера и формы площадки контакта, а также распределения нормальных контактных напряжений. Результаты решения нормальной задачи используются для нахождения решения тангенциальной, заключающейся в нахождении распределения касательных напряжений и момента в зонах сцепления и проскальзывания контактной площадки.
Г. Герц дал первое надежное математическое решение нормальной
задачи, которая формулируется следующим образом. Два ненагруженных тела (поверхности
катания колеса и рельса) касаются в одной точке. Расстояние между недеформированными
телами может быть найдено геометрически, если известны радиусы кривизны тел в
точке контакта. Упругие свойства колеса и рельса, описываемые коэффициентом
Пуассона 
и
модулем упругости 
, считаются одинаковыми. Если
тела нагружены нормальной силой 
, появляется зона контакта
эллиптической формы с большой полуосью в направлении продольной оси рельса
представленной на рис. 5.
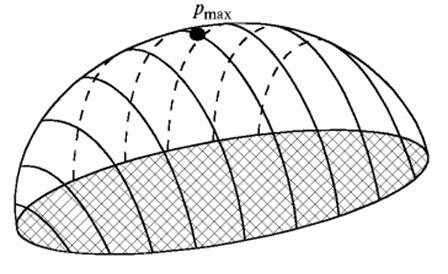
Рисунок 5 - Распределение нормальных герцевских напряжений на площадке контакта
Максимальное контактное напряжение 
может быть рассчитано по формуле:
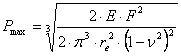(1)
где 
– эквивалентный радиус,
зависящий от характерных радиусов взаимодействующих тел (колеса и рельса) в
месте контакта.
Таким образом, нормальное напряжение на поверхностях катания рельса и колеса зависит от нагрузки от колеса на рельс, радиусов поверхностей катания колеса и рельса, свойств взаимодействующих материалов.
Следует иметь в виду, что контактная теория Герца справедлива при следующих допущениях:
· контактирующие поверхности однородны и изотропны;
· силы трения в зоне контакта не действуют;
· размер контактной площадки мал по сравнению с размерами контактирующих тел и характерными радиусами кривизны недеформированных поверхностей;
· для контактной задачи использовано решение линейного упругого полупространства;
· контактирующие поверхности гладкие.
При движении экипажа положение колесной пары по отношению к рельсам существенно меняется, приводя к возникновению различных сочетаний контактных зон колеса и рельса.
Даже при условии постоянной осевой нагрузки нормальные напряжения будут существенно меняться из-за различия в радиусах кривизны контактирующих поверхностей этих зон.
Если в области контакта имеет место один радиус кривизны
поверхности, можно использовать решение Герца. Если в области контакта имеются
два или несколько радиусов кривизны, например 
и 
(рис. 6.), решение Герца несправедливо,
и для определения площадки контакта следует использовать негерцевское решение.
Это особенно важно при разнообразных сочетаниях изношенных профилей колеса и
рельса.
При нахождении нормальных контактных напряжений для неконформного негерцевского контакта используются различные методы и программы. В частности, полное решение негерцевской задачи может быть найдено с помощью программы CONTACT [6]. Однако из-за того, что решение задачи с помощью этой программы требует большого времени, предложены различные варианты приближенного решения негерцевской задачи. Например, с использованием метода аппроксимации негерцевской геометрии эллипсами получены результаты, в достаточной мере согласующиеся с точным решением (рис. 7.) [7].
Другой подход, используемый для нахождения контактных напряжений между изношенными колесом и рельсом, состоит в моделировании контактирующих тел с использованием упругого винклеровского основания, при котором деформация поверхностей пропорциональна нормальным контактным напряжениям [8]. Полученное при этом максимальное контактное напряжение будет в 1,3 больше, чем при герцевском решении. Размер площадки контакта и распределение нормальных напряжений зависят от нормальной нагрузки, действующей от колеса на рельс, профилей колеса и рельса, поперечного и углового положения колесной пары на рельсах и подуклонки рельсов.
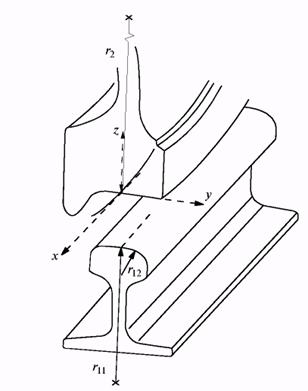
Рисунок 6 - Геометрия контакта колеса и рельса:
– оси системы координат; 
–
характерные радиусы (
– радиус профиля колеса)
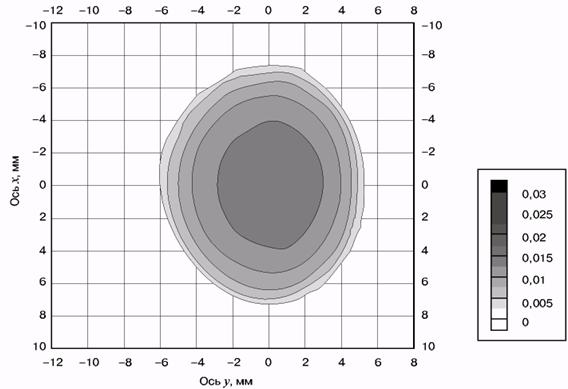
Рисунок 7 - Форма площадки контакта и распределение давлений:
Когда колесная пара движется в кривой, при определенном угле набегания колесо может контактировать с рельсом в двух различных точках [9]. Двухточечный контакт приводит к образованию двух площадок контакта: А на поверхности катания рельса и В на боковой поверхности головки рельса в районе выкружки (рис. 8.,а). Из-за того что колесная пара при движении в кривой перемещается с некоторым углом набегания а, площадка контакта В сдвинута вперед (рис. 8.,б). Увеличение угла набегания приводит к увеличению расстояний между площадками контакта (забега) и до мгновенной оси вращения колесной пары и тем самым к возрастанию относительного проскальзывания и тангенциальной силы, с ним связанной. В зоне касания гребня колеса и рабочей грани головки наружного рельса уровень расчетных контактных напряжений может достигать 3000 МПа.
При контакте сильно изношенного рельса с новым или изношенным колесом изменяется форма области распределения давлений. Размер площадки контакта существенно уменьшается, она сдвигается к внешней поверхности наружного рельса, приводя к увеличению контактных давлений, уровень которых может достигать предела текучести, что вызывает пластическую деформацию головки рельса.
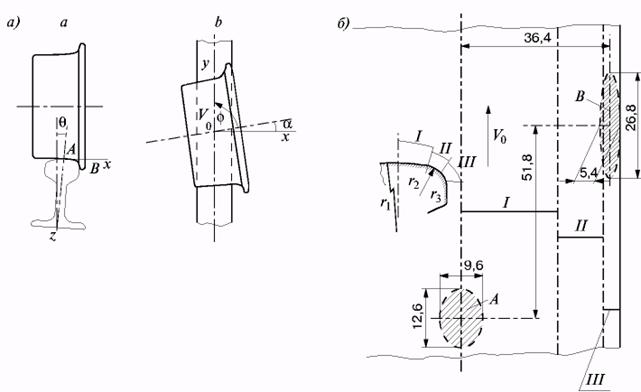
Рисунок 8 - Положение и размеры
контактных площадок при двухточечном контакте колеса и рельса 
:
а) А, В – точки контакта колеса с
рельсом; –
оси координат
– угол набегания колеса на
рельс; 
–
угол подуклонки рельса; 
– вектор скорости движения
колесной пары б) А, В – площадки контакта; I, II, III
– области контакта; 
– радиусы кривизны головки
рельса
Обычно контактные напряжения на поверхности катания (область А) колеса грузового вагона находятся в пределах 1300 – 1700 МПа. Увеличение осевой нагрузки приводит к возрастанию герцевских контактных напряжений пропорционально степени 1/3 от ее величины (см. формулу 1).
Если поверхность катания колеса имеет прокат с образовавшимся корытообразным поперечным профилем, это приводит к существенному увеличению контактных давлений, которые могут иметь место по обеим сторонам этого профиля. Так, при величине проката корытообразного профиля 2 мм расчетные контактные напряжения на обоих краях могут достигать 6000 МПа, что свидетельствует о значительном пластическом течении материалов.
Высокие контактные напряжения возникают в случаях, если профиль колеса своим внешним краем будет опираться на рельс или контактная зона не достигает внешнего края колеса, приводя к возникновению выступа (фальшивого гребня) в области наружной части поверхности катания колеса.
Величина и распределение контактных напряжений существенно зависят от профилей колеса и рельса и от того, какой имеет место контакт: одноточечный или двухточечный. При конформном профиле размер площадки контакта увеличивается, приводя к уменьшению уровня контактных напряжений по сравнению с неконформными профилями.
Таким образом для оценки общего напряженного состояния в паре колесо-рельс достаточно решить задачу Герца для одноточечного контакта бандажа и рельса. Решение задачи производилось в программном комплексе ANSYS.
При построении модели “колесо – рельс” и проведении расчетов рассматривался тип рельса Р65 по ГОСТ 18267 – 82, и бандаж ГОСТ 398 – 96, при этом рассматривался неизношенный профиль бандажа и рельса. Механические свойства бандажа и рельса, используемые для расчета представлены в таблице 1.
Таблица 1 - Механические свойства бандажа и рельса
|
Механические свойства |
Бандаж ГОСТ 398 – 96 |
Рельс ГОСТ 18267 – 82 |
|
Плотность, кг/м3 |
7850 |
7850 |
|
Модуль Юнга, Па |
|
|
|
Коэффициент Пуассона |
0,3 |
0,3 |
Схема сил, загружающих колесную пару, представлена на рисунке 9.
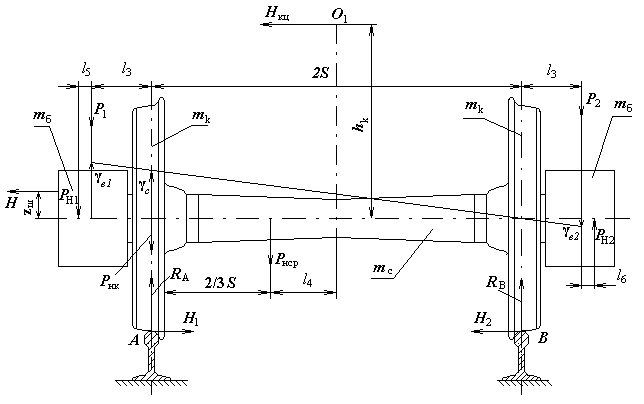
Рисунок 9 - Схема сил, загружающих колесную пару
В глобальной декартовой системе координат производилось разбиение колесной пары на тетроэдральные конечные элементы. Конечноэлементная сетка представлена на рисунке 10.
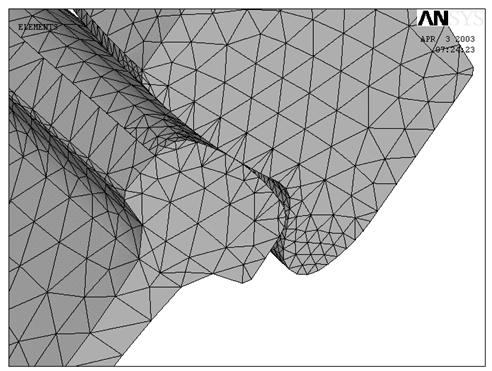
Рисунок 10- Конечноэлементная модель пары “Колесо - рельс”
На рисунке 11 представлена эпюра распределения напряжений в паре “колесо - рельс”.
Рисунок 11- Эпюра распределения напряжений в контакте пары “Колесо - рельс”
При расчете было выявлено, что в зоне контакта на поверхности катания колеса напряжения достигают значительных величин, но они локализованы в пределах небольшой области. Размер этой области соизмерим с размером пятна контакта.
Выводы
1. Установление оптимальной твердости поверхности катания колеса представляет собой сложную задачу, решение которой должно осуществляться системно с учетом, различных параметров.
2. Твердость поверхности катания колес в настоящее
время ограничена величиной .
3. Напряжения локализованы в пределах малой области колеса и рельса. Размер области соизмерим с размером пятна контакта.
1. Шур Е. А. К вопросу об оптимальном соотношении твердости рельсов и колес //Современные проблемы взаимодействия подвижного состава и пути: Материалы научно-практической конференции/ ВНИИЖТ. – М., 2003. с. 87 – 93.
2. Бартенева Л. И. Технология лубрикации боковой поверхности рельсов передвижными рельсосмазывателями – комплексное решение проблемы износа в контакте гребень колеса – рельс //Современные проблемы взаимодействия подвижного состава и пути: Материалы научно-практической конференции/ ВНИИЖТ. – М., 2003. с. 114 – 122.
3. Шур Е.А., Бычкова Н.Я., Марков Д.П., Кузьмин Н.Н. Износостойкость рельсовых и колесных сталей // Трение и износ. Том 16. – 1995. №1. с. 80 – 91.
4. Ларин Т. В. Об оптимальной твердости элементов пары трения «колесо – рельс» // Вестник ВНИИЖТ, 1965. - №3. с. 5-9.
5. Вихрова А. М., Ларин Т. В., Парышев Ю. М., Хургин Л. С. О соотношении твердости рельсовой и колесной стали // Вестник ВНИИЖТ. 1983 №6 с. 34 – 38.
6. B. Paul, J. Hashemi. User's Manual for Program CONTACT. Technical Report No. 4, FRA/ORD-78/27/PB286097, NTIS, Springfield, VA, Sept. 1977.
7. R. Harder. Creep Force – Creepage and Frictional Work Behaviour in Non-Hertzian Counter formal Rail/Wheel Contacts. Proceedings of IHHA'99 STS-Conference on Wheel/Rail Interface. Moscow, 1999, V. 1, p. 207 – 214.
8. I. Goryacheva. Contact Mechanics in Tribology. Kluver Academic Publishers.
9. А. Я. Коган. Динамика пути и его взаимодействие с подвижным составом. М.: Транспорт, 1997, 326 с.